Speaker
Description
There exist many models of physics beyond the Standard model (SM) which introduce new heavy particles. Signals of such new states could be parametrized either within a complete model of new physics or its low-energy approximation. The latter consists of effective Lagrangian (EL), which describes effects of interactions with heavy particles on the dynamics of light fields when heavy states decouple. Parameters of this EL should be constrained in experimental data analysis. These constraints, in turn, are translated into limits on parameters of a corresponding complete model. This approach is employed in many researches. In our investigation we show that the EL considered in this treatment is valid only if loop corrections coming from the light sector of a corresponding complete model are negligible in the decoupling limit.
Our research is conducted for two scattering processes which take place in $s$- and $t$-channel, respectively. Transformational properties of fields and complex interactions within the SM are inessential for our analyzis. Hence, we consider generalized Yukawa model instead of a complete SM extended with some new states. We begin with the following Lagrangian of a complete model:
$$\begin{equation}
\mathcal{L} = \frac{1}{2}\left(\partial_{\mu}\phi\right)^2 - \frac{1}{2}\mu^2\phi^2 + \frac{1}{2}\left(\partial_{\mu}\chi\right)^2 - \frac{1}{2}\Lambda^2\chi^2 - \lambda\phi^4 - \rho\phi^2\chi^2 - \xi\chi^4 +
\\ +\sum\limits_{a=1;2}\bar{\psi}_a\left(i\hat{\partial} - m_a - g_{\phi}\phi - g_{\chi}\chi\right)\psi_a
\end{equation}.~~ (1)$$
This model consists of two scalar fields $\phi$ and $\chi$ and two fermionic fields $\psi_1$ and $\psi_2$. We put $\chi$ boson to be much heavier than the other particles of the model, so $\Lambda\gg \mu;\,m_1;\,m_2$. We derived the following low-energy EL for this model in the limit when $\chi$ boson decouples:
$$\begin{equation}
\mathcal{L}_{eff} = \frac{1}{2}\left(\partial_{\mu}\phi\right)^2 - \frac{1}{2}\mu^2\phi^2 - \lambda\phi^4 + \sum\limits_{a=1;2}\bar{\psi}_a\left(i\hat{\partial} - m_a - g_{\phi}\phi\right)\psi_a + \frac{g_{\chi}^2}{2\Lambda^2}\left(\bar{\psi}_1\psi_1 + \bar{\psi}_2\psi_2\right)^2.
\end{equation}~ (2)$$
Here the last term describes effective four-fermion interactions which approximate contributions of the heavy scalar in observables when $\chi$ decouples. The other terms in (2) describe dynamics of the model light sector if $g_{\chi} = 0$.
Two scattering processes were considered within the complete model (1) and EFT (2) - these are $\psi_1\bar{\psi_1} \rightarrow \psi_2\bar{\psi_2}$ and $\psi_1\psi_2 \rightarrow \psi_1\psi_2$. Cross-sections of these processes were derived within the complete model (1) in the improved Born approximation and within the EFT (2). Contributions of radiative corrections into the cross-sections of these processes were estimated in the decoupling limit. We investigated scenarios where $\chi$ boson has a mass in the interval $20\mu \leq \Lambda \leq 200\mu$.
(a) Loop corrections to the $\phi$ boson mass
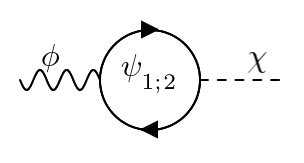(b) Diagram of one-loop mixing of light and heavy scalars of
the model
FIG. 1: One-loop diagrams which become significant at low energies for some values of the model coupling.
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~$
We found out that if $|g_{\phi}|$ and $|g_{\chi}|$ are small, then the loop corrections are negligible and the EL (2) is applicable for description of the scattering processes at low energies. For the values of $m_1$, $m_2$ and $\mu$ chosen in our research this takes place if $|g_{\phi}| < 0.4$ and $|g_{\chi}| < 0.4$.
If $|g_{\chi}|$ is big, then loop corrections to $\chi$ boson mass are considerable even at low energies. In our model, we have that if $|g_{\chi}| > 2.5$ then corrections displayed in Fig.(1a) have a magnitude of more than $10\,\%$ of the $\chi$ boson mass. These corrections suppress the contribution of the heavy scalar in a reaction cross-section. Hence, if $|g_{\chi}|$ is big, then (2) significantly overestimates $\chi$ boson contribution in a cross-section when $\chi$ decouples.
If $|g_{\phi}|$ is not small, then contribution of the scalar fields one-loop mixing is significant in both $s$- and $t$-channels. One-loop mixing of $\phi$ and $\chi$ is introduced by the diagram in Fig.(1b). In our model, we get that if $|g_{\phi}| > 1.5$, then modulus of the contribution of scalars one-loop mixing in the matrix elements of the considered reactions is bigger than $50\,\%$ of the four-fermion interaction term modulus at $s > \mu^2$ and $|t| > \mu^2$. This was observed in the limit when loop correction in Fig.(1a) is negligible.
To conclude, in our research we have derived the conditions when radiative corrections to interactions with the heavy boson are negligible in the decoupling limit in cross-sections of reactions within the generalized Yukawa model. According to these conditions, radiative corrections become significant if the interactions between light fermions and either light or decoupled scalar are not feeble. In such scenarios, expression (2) should not be used as the low-energy approximation of the model (1). The results obtained in this investigation could be applied to some models of new physics which extend the SM, such as the two-Higgs-doublet model (2HDM). The latter has a limit when new heavy particles decouple. So, low-energy EL exists for it. Contributions of radiative corrections into cross-sections within the 2HDM should be estimated in the limit when heavy fields beyond the SM decouple. This is the problem left for the future.
