XIV Conference of Young Scientists "Problems of Theoretical Physics"
BITP & Zoom
Dedicated to the 115th anniversary of the outstanding theoretician in the physical sciences and mathematician M.M. Bogolyubov (1909-1992)
Organizing committee is greeting the participants with the best presentations at the conference:
Yulian Honchar “How partition function zeros help find out the finite-size scaling above the upper critical dimension” (Institute for Condensed Matter Physics, NAS of Ukraine, Lviv)
Mykola Yelisieiev “Theory of low-frequency electron fluctuations in a quasi-ballistic FET” (Institute of Semiconductor Physics, NAS of Ukraine, Kyiv)
Yurii Zhuravlov “Long-time asymptotic series for the Painleve II equation: Riemann- Hilbert approach” (Bogolyubov Institute for Theoretical Physics, NAS of Ukraine, Kyiv)
Musfer Adzhymambetov “Dynamic Picture of Relativistic Heavy-Ion Collisions” (Bogolyubov Institute for Theoretical Physics, NAS of Ukraine, Kyiv)
TOPICS OF THE CONFERENCE
High energy physics, astroparticle physics, quantum cosmology, theory of nuclear systems, quantum field theory, theory of symmetries, theory of nonlinear processes in macromolecular structures, nanosystems and plasmas, dynamics of open strongly nonequilibrium physical, biological, economic and information systems.
SECTIONS
- Astrophysics and Cosmology
- Mathematical Physics
- Statistical Theory of Many-body Systems
- Physics of Biological Macromolecules
- Condensed Matter Physics
- Physics of Nuclei and Elementary Particles
The lectures of leading scientists will be presented in each section.
We invite undergraduate and postgraduate students and young scientists. The maximum age of a participant is 35. The working language of the Conference is English. We provide 20 min for an oral talk. Proceedings of the best talks will be recommended for publishing in the Ukrainian Journal of Physics.
The following event will be held in hybrid format: offline in Kyiv, Ukraine and online based on the Zoom platform.
No conference fee is charged for participation.
The deadline for abstract submission is January 9 2024.
ORGANIZING COMMITTEE
Head – Academician of NAS of Ukraine, Prof Dr. Anatoly Zagorodny;
Ph.D. Ivan Starodub; Ph.D. Sergiy Perepelytsya; Ph.D. Denys Savchenko; Ph.D. Dmytro Piatnytskyi
-
-
-
Quantum logic gates applied to qubits are basic elements of the circuit model used for quantum computations. Usually, quantum gates are realized by a resonant excitation, resulting in Rabi oscillations, which lead to a periodic excitation of the qubit. It has certain limitations and complications, like neglecting counter-rotating terms. We investigate an alternative way for quantum control and performing of quantum logic gates with Landau-Zener-Stückelberg-Majorana (LZSM) transitions [1,2,3] using nonadiabatic driving and alternation of the two stages of evolution: adiabatic evolution and non-adiabatic transitions. We investigate mechanisms, dynamics, and ways to optimize single-qubit LZSM gates [1,3]. We apply the adiabatic-impulse model to describe multiple LZSM transitions [1,3], which we use to create LZSM-based quantum logic gates. Any single-qubit operation can be realized with only two LZSM transitions with an adjustable time of free evolution time before and after those transitions. To gain better fidelity and reduce quantum gates performing time, we can use multiple LZSM transitions. LZSM-based quantum logic gates in comparison with Rabi oscillations based gates allow us to reduce gate time with keeping fidelity high, enabling us to perform more gates before the impact from decoherence and relaxation becomes significant. Fig.1 shows the dynamics for the NOT (X) gate realized by double LZSM transitions.
Acknowledgments: This research was funded by the Army Research Office and was supported by Grant No. 911NF-20-1-0261, RIKEN International Program Associate.- A. Ryzhov, O. Ivakhnenko, S. Shevchenko, «Alternative fast quantum logic gates using nonadiabatic Landau-Zener-Stückelberg-Majorana transitions», ArXiv:2310.17932, 2023
- D. Campbell, et al., «Universal nonadiabatic control of small-gap superconducting qubits», Phys. Rev. X, 2020 10, 041051
- O. V. Ivakhnenko, S. N. Shevchenko and F. Nori «Nonadiabatic Landau-Zener-Stückelberg-Majorana transitions, dynamics, and interference», Phys. Rep., 2023, 995, 1.
Fig. 1. Dynamics for the NOT (X) gate with ground initial state with double LZSM transitions: (a) dynamics on the Bloch sphere, (b) dynamics of Bloch coordinates.Speaker: Dr Oleh Ivakhnenko (B. Verkin ILTPE of NASU | RIKEN, Japan)
-
-
-
-
-
In this paper, a computer simulation of radiation-induced segregation in the Fe-20Cr-8Ni alloy was carried out within the framework of the modified inverse Kirkendall model [1-3]. The dependences of the concentrations of Cr and Ni atoms on the surface of the sample on the rate of production of point defects and temperature, as well as the concentration profiles of Cr and Ni atoms and point defects, were calculated. The influence of the rate of production of point defects and temperature on the concentration profiles of components and point defects is analyzed in detail. It is shown that the effect of the increase in the rate of production of point defects on the concentration profiles of the alloy components can be compensated with a sufficiently high accuracy by a relatively small increase in temperature (fig. 1). This effect is explained by the competition of two mechanisms: (i) increasing the irradiation of the alloy leads to a narrowing of the concentration profiles; (ii) an increase in temperature leads to a broadening of concentration profiles.
Fig. 1. Concentration profiles of Cr and Ni in the Fe-20Cr-8Ni alloy under irradiation.- G.S. Was, Fundamentals of Radiation Materials Science. Metals and Alloys (2nd ed.) (New York: Springer: 2017).
- R.V. Skorokhod, O.M. Buhay, V.M. Bilyk, V.L. Denysenko and O.V. Koropov, East European Journal of Physics, 5, No. 1: 61–69 (2018) (in Ukrainian).
- R.V. Skorokhod and O.V. Koropov, Metallofiz. Noveishie Tekhnol., 44, No. 6: 691—711 (2022) (in Ukrainian).
Speaker: Roman Skorokhod (Institute of Applied Physics of National Academy of Sciences of Ukraine, Sumy, Ukraine)
-
-
-
There exist many models of physics beyond the Standard model (SM) which introduce new heavy particles. Signals of such new states could be parametrized either within a complete model of new physics or its low-energy approximation. The latter consists of effective Lagrangian (EL), which describes effects of interactions with heavy particles on the dynamics of light fields when heavy states decouple. Parameters of this EL should be constrained in experimental data analysis. These constraints, in turn, are translated into limits on parameters of a corresponding complete model. This approach is employed in many researches. In our investigation we show that the EL considered in this treatment is valid only if loop corrections coming from the light sector of a corresponding complete model are negligible in the decoupling limit.
Our research is conducted for two scattering processes which take place in $s$- and $t$-channel, respectively. Transformational properties of fields and complex interactions within the SM are inessential for our analyzis. Hence, we consider generalized Yukawa model instead of a complete SM extended with some new states. We begin with the following Lagrangian of a complete model:
$$\begin{equation} \mathcal{L} = \frac{1}{2}\left(\partial_{\mu}\phi\right)^2 - \frac{1}{2}\mu^2\phi^2 + \frac{1}{2}\left(\partial_{\mu}\chi\right)^2 - \frac{1}{2}\Lambda^2\chi^2 - \lambda\phi^4 - \rho\phi^2\chi^2 - \xi\chi^4 + \\ +\sum\limits_{a=1;2}\bar{\psi}_a\left(i\hat{\partial} - m_a - g_{\phi}\phi - g_{\chi}\chi\right)\psi_a \end{equation}.~~ (1)$$ This model consists of two scalar fields $\phi$ and $\chi$ and two fermionic fields $\psi_1$ and $\psi_2$. We put $\chi$ boson to be much heavier than the other particles of the model, so $\Lambda\gg \mu;\,m_1;\,m_2$. We derived the following low-energy EL for this model in the limit when $\chi$ boson decouples: $$\begin{equation} \mathcal{L}_{eff} = \frac{1}{2}\left(\partial_{\mu}\phi\right)^2 - \frac{1}{2}\mu^2\phi^2 - \lambda\phi^4 + \sum\limits_{a=1;2}\bar{\psi}_a\left(i\hat{\partial} - m_a - g_{\phi}\phi\right)\psi_a + \frac{g_{\chi}^2}{2\Lambda^2}\left(\bar{\psi}_1\psi_1 + \bar{\psi}_2\psi_2\right)^2. \end{equation}~ (2)$$ Here the last term describes effective four-fermion interactions which approximate contributions of the heavy scalar in observables when $\chi$ decouples. The other terms in (2) describe dynamics of the model light sector if $g_{\chi} = 0$. Two scattering processes were considered within the complete model (1) and EFT (2) - these are $\psi_1\bar{\psi_1} \rightarrow \psi_2\bar{\psi_2}$ and $\psi_1\psi_2 \rightarrow \psi_1\psi_2$. Cross-sections of these processes were derived within the complete model (1) in the improved Born approximation and within the EFT (2). Contributions of radiative corrections into the cross-sections of these processes were estimated in the decoupling limit. We investigated scenarios where $\chi$ boson has a mass in the interval $20\mu \leq \Lambda \leq 200\mu$.
(a) Loop corrections to the $\phi$ boson mass
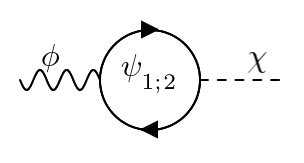(b) Diagram of one-loop mixing of light and heavy scalars of
the model
FIG. 1: One-loop diagrams which become significant at low energies for some values of the model coupling.
$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~$
We found out that if $|g_{\phi}|$ and $|g_{\chi}|$ are small, then the loop corrections are negligible and the EL (2) is applicable for description of the scattering processes at low energies. For the values of $m_1$, $m_2$ and $\mu$ chosen in our research this takes place if $|g_{\phi}| < 0.4$ and $|g_{\chi}| < 0.4$.
If $|g_{\chi}|$ is big, then loop corrections to $\chi$ boson mass are considerable even at low energies. In our model, we have that if $|g_{\chi}| > 2.5$ then corrections displayed in Fig.(1a) have a magnitude of more than $10\,\%$ of the $\chi$ boson mass. These corrections suppress the contribution of the heavy scalar in a reaction cross-section. Hence, if $|g_{\chi}|$ is big, then (2) significantly overestimates $\chi$ boson contribution in a cross-section when $\chi$ decouples.
If $|g_{\phi}|$ is not small, then contribution of the scalar fields one-loop mixing is significant in both $s$- and $t$-channels. One-loop mixing of $\phi$ and $\chi$ is introduced by the diagram in Fig.(1b). In our model, we get that if $|g_{\phi}| > 1.5$, then modulus of the contribution of scalars one-loop mixing in the matrix elements of the considered reactions is bigger than $50\,\%$ of the four-fermion interaction term modulus at $s > \mu^2$ and $|t| > \mu^2$. This was observed in the limit when loop correction in Fig.(1a) is negligible.To conclude, in our research we have derived the conditions when radiative corrections to interactions with the heavy boson are negligible in the decoupling limit in cross-sections of reactions within the generalized Yukawa model. According to these conditions, radiative corrections become significant if the interactions between light fermions and either light or decoupled scalar are not feeble. In such scenarios, expression (2) should not be used as the low-energy approximation of the model (1). The results obtained in this investigation could be applied to some models of new physics which extend the SM, such as the two-Higgs-doublet model (2HDM). The latter has a limit when new heavy particles decouple. So, low-energy EL exists for it. Contributions of radiative corrections into cross-sections within the 2HDM should be estimated in the limit when heavy fields beyond the SM decouple. This is the problem left for the future.
Speaker: Mykyta Dmytriiev (Oles Honchar Dnipro National University)
-
-