Speaker
Description
The Standard Model (SM) is a particle physics theory that is consistent up to very high energy scales and verified in numerous experiments up to $\sim 14$ TeV. However, it fails to explain some phenomena such as massiveness of neutrinos, dark matter, dark energy, baryon asymmetry of the Universe etc. Therefore, SM is incomplete and requires an extension.
One possible approach is by adding new particles to the theory. There are two possible answers to the question "Why do we not observe particles of new physics in experiments?" The first answer is the following. The new particles are very heavy and can not be produced in modern accelerators like LHC. To detect them one has to build more powerful and more expensive accelerators. There is another possibility. The particles of new physics can be light particles that feebly interact with SM particles.
The last case is very interesting for the experimental search of the new physics just now. There are three possible choices of new renormalized interaction Lagrangian of particles of new physics with SM particles. It's called portals. There are scalar portal, heavy neutral leptons portal, vector portal. There are other portals of high-dimensional operators such as portal of pseudoscalar particles (axion-like particles), or Chern-Simons like (parity odd) interaction of electroweak gauge bosons with a new vector field [1].
In this paper, we consider a Chern-Simons (CS) portal with new neutral vector particle ($X$) boson.
This extension has not yet been studied sufficiently. This interaction was proposed in [2]. It origins from non-trivial anomaly cancellations in theory with new heavy fermions. It has gauge-invariant form
$$
\mathcal{L}_1=\frac{C_Y}{\Lambda_Y^2}\cdot X_\mu (\mathfrak D_\nu H)^\dagger H B_{\lambda\rho} \cdot\epsilon^{\mu\nu\lambda\rho}+h.c., \quad
\mathcal{L}_2=\frac{C_{SU(2)}}{\Lambda_{SU(2)}^2}\cdot X_\mu (\mathfrak D_\nu H)^\dagger F_{\lambda\rho} H\cdot\epsilon^{\mu\nu\lambda\rho}+h.c.
$$
In the low energy limit (unitary gauge) the effective renormalized Lagrangian of three particle interaction CS boson with SM particles is
$$
\mathcal{L}_{CS}=c_z \epsilon^{\mu\nu\lambda\rho} X_\mu Z_\nu \partial_\lambda Z_\rho +c_\gamma \epsilon^{\mu\nu\lambda\rho} X_\mu Z_\nu \partial_\lambda A_\rho+\left\{ c_w \epsilon^{\mu\nu\lambda\rho} X_\mu W_\nu^- \partial_\lambda W_\rho^+ + h.c.\right\}.
$$
For the experimental search of the new particle, it is very important to theoretically consider channels of production and decay of the new particle. We consider the case of experiments on Cern SPS accelerator, where CS particles can not be produced from the decay of real $W$, $Z$ bosons. In this paper, we consider the production of CS GeV-scale particles in mesons' decay.
To do it we get effective Lagrangian of CS interaction with different quarks due to presented here loop diagram in the form
$$
\mathcal{L}_{CSd}= \sum_{m\neq n}\Theta_{1W}\left( C^d_{mn}\, \bar{\Psi}_{d_n}\, \gamma^{\mu}\,\hat
P_L \, \Psi_{d_m} X_{\mu}+h.c.\right)%-\sum_n\Theta_W^1 g^2 C^d_{nn}\, \bar{\Psi}_{d_n}\, \gamma^{\mu}\,\hat P_L \, \Psi_{d_n} X_{\mu},
$$
where $\Theta_{1W}$ is real part of $c_w$ coupling and $C^d_{bs}=1.97\cdot 10^{-4}$, $C^d_{bd}=4.43\cdot 10^{-5}$, $C^d_{sd}=1.77\cdot 10^{-6}$.
As it turned out the loop with different quarks does not suffer from divergence problem and we have to take into account only interaction with down quarks, because coefficients of interaction with up quarks are sufficiently smaller.
So, we will consider CS particle production in meson's decay only due to decay of heavy down quark in the meson.
Initial lightest mesons containing $b$ and $s$ quarks are $B$-mesons and $K^\pm$, $K^0_S$, $K^0_L$ mesons.
Possible reaction of $B$-meson decay with $X$-particle production is decay into pseudoscalar mesons ($K$ and $\pi$ mesons), scalar mesons ($K^{0\star}(700)$, $K^{0\star}(1430)$), vector mesons ($K^\star(892)$, $K^\star(1410)$, $K^\star(1680)$), pseudovector mesons ($K_1(1270)$, $K_1(1400)$) and tensor final meson states ($K_2(1430)$).
For the initial kaons states, the only possible 2-body decay is the process $K \to \pi +X$.
There are 3 types of the kaons: $K^{\pm}$, $K^0_L$, $K^0_S$. Since $K^0_S$ is the $CP$-even eigenstate, the decay $K^0_S\to \pi S$ is proportional to the CKM $CP$-violating phase and is strongly suppressed. Further we assume that the corresponding branching ratio vanishes and consider only reactions $K^\pm \to \pi^\pm +X$ and $K^0_L \to \pi^0 +X$.
The amplitude of $h$-meson decay into $h'$-meson and $X$-particle has the form
$$
M_{h\rightarrow h'X}=\Theta_{1W} C^d_{mn} \, \langle h'(p'))|\bar d_n\gamma^{\mu} \hat P_L d_m|h(p)\rangle\,
\epsilon^{\star\lambda_X}_{\mu}.
$$
This quantity can be obtained with help of formalism summarised in [3].
In the following, we plan to complete consideration of the production of CS particles by examining direct CS production in $p-p$ collisions. Also, we plan to consider possible channels of CS particles' decay.
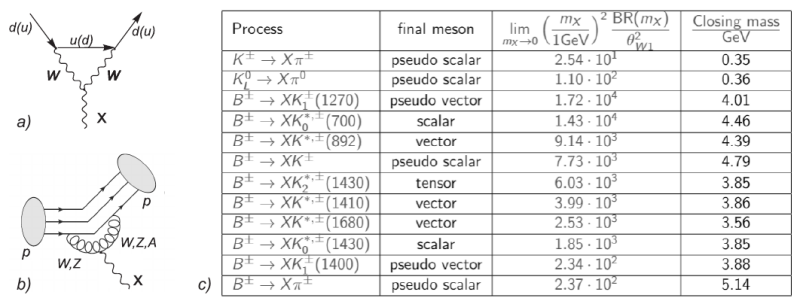Figure 1. a) loop diagram of quarks interactions with CS particles; b) diagram of CS production in meson's decay c) decay of $B$- and $K$-mesons with CS production.
[1] Sergey Alekhin et al. A facility to Search for Hidden Particles at the CERN SPS: the SHiP physics case. Rept. Prog. Phys., 79(12):124201, 2016.
[2] Ignatios Antoniadis, Alexey Boyarsky, Sam Espahbodi, Oleg Ruchayskiy, and James D.Wells. Anomaly driven signatures of new invisible physics at the Large Hadron Collider. Nucl. Phys., B824:296–313, 2010.
[3] Iryna Boiarska, Kyrylo Bondarenko, Alexey Boyarsky, Volodymyr Gorkavenko, Maksym Ovchynnikov, and Anastasia Sokolenko. Phenomenology of GeV-scale scalar portal. JHEP, 11:162, 2019.
