Speaker
Description
When we drive quantum two-level systems (or qubits) by periodical signals, we obtain repeatedly Landau-Zener-Stückelberg-Majorana (LZSM) transitions, which relates to the tunneling in qubits [1]. Recent interest for studying these repeated transitions is caused by the success in creation of the first quantum computing machines which are based on different types of connected driven qubits. We describe a transfer matrix (TM) approach [2], and its area of usability, for a single LZSM transition which started from a superpositional state. As the result, we obtain a formula for describing the final occupation probability with any superpositional initial state. We consider three types of a single transition, with: 1. Constructive interference, 2. Destructive interference, and 3. Occupation-conservation transition. The last one allows us to save the same occupation probability as before the transition. TM can also be used for describing repetitive transitions by using the result of the current transition as the initial condition for the next one. Previously in Ref. [3] the "transitionless transitions" in qubits were studied, there the author described only the case when initially a qubit was not in any superpositional state, but rather only in one of the basis states. In Fig. 1 we demonstrate constructive and destructive transition in comparison with numerical and analytic solution on the left side and occupation conservation case in the right panel, where also we demonstrated the range of possible final occupation probabilities.
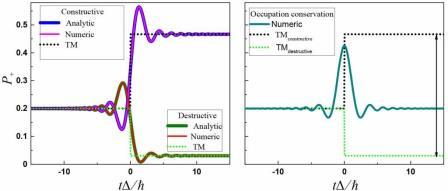
Fig. 1. (left) Constructive and destructive LZSM transitions, (right) Occupation-conservation transition, where the probability after passing the avoided-level crossing is exactly the same as it was initially. Both panels are plotted with the same initial conditions $P_{+i}=0.2$, the same parameters defining the transition probability, if starting from the ground state, $P_{LZSM}=0.081$, and with the initial phase difference $\phi_i$ being different in each case.
Acknowledgment:
Research of O.V.I. and S.N.S. is sponsored by the Army Research Office and is accomplished under Grant Number W911NF-20-1-0261.
[1] O.V. Ivakhnenko, S.N. Shevchenko, and F. Nori «Landau-Zener-Stückelberg-Majorana (LZSM) transitions for interferometry and quantum control», in preparation.
[2] B. Damski and W. H. Zurek, «Adiabatic-impulse approximation for avoided level crossings: from phase-transition dynamics to Landau-Zener evolutions and back again», Phys. Rev. A 73, 063405 (2006).
[3] M. V. Berry, «Transitionless quantum driving», J. Phys. A: Math. Theor. 42, 365303 (2009).
