Speaker
Description
An emerging field of curvilinear magnetizm brings about new geometry-induced phenomena in usual magnetic materials, balancing between fundamental research, material sciences and technologies [1]. Modern technological advances allow to consider antiferromagnets (AFMs) as promising building blocks for spintronic and spin-orbitronic applications [2]. In this respect, curvilinear spin chains with AFM coupling are of fundamental interest as simplest systems possessing interplay between geometry and magnetic subsystem.
Here, we analyze the ground states of AFM ring with the nearest-neighbour Heisenberg exchange and strong single-ion anisotropy in the presence of external magnetic field, which is normal to the ring plane. We consider collinear two-sublattice 1D curved AFM spin chain with even number of spins. The hard axis of anisotropy is oriented tangentially to the chain. Within the classical continuum approach [3], its magnetic state is determined by the vector fields of Néel and ferromagnetism. In the ground state, the Néel vector is oriented perpendicularly to the ring plane (binormal state, see Fig.1) [3,4]. The magnetic field applied along the ring normal allows to observe spin-flop and spin-flip orientational phase transitions. We determine the dependency of spin-flop and spin-flip transition fields on the ring curvature. There is a critical curvature ($\kappa_c$), separating two topologically different ground states above spin-flop. The first one with the Néel order parameter within the normal plane is mainly determined by the anisotropy at small curvatures (normal state, see Fig.1). The second ground state at large curvatures is represented by oninon ordering of the Néel vector (onion state, see Fig.1). With the applied fields $h>h^0$, Néel order parameter vanishes (ferromagnetic state). The phase diagram of AFM as a function of applied field intensity is presented in Fig.1: all analytical predictions are well-confirmed by the SLaSi spin-lattice simulations [5].
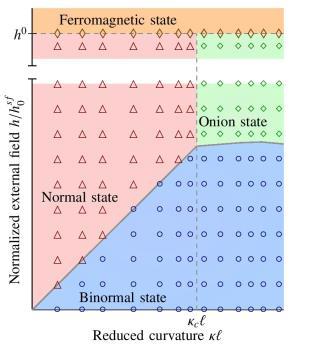
Fig.1: phase-diagram.jpg should be here, with
caption: "Phase diagram of equilibrium magnetization states of antiferromagnetic ring; $h^{sf}_0$ is the spin-flop transition field in the bulk, $\kappa$ is the ring curvature, $\ell = 5 a_0$ is the magnetic length, with $a_0$ being the lattice constant. Symbols correspond to spin-lattice simulation data, solid lines describe analytically calculated boundary between states"
[1] E.Vedmedenko et al, Journal of Physics D: Applied Physics 53, 453001(2020).
[2] V. Baltz et al, Reviews of Modern Physics 90, 015005 (2018)
[3] O. V. Pylypovskyi et al, Nano Letters 20, 8157 (2020)
[4] S. Castillo-Sepulveda et al, Physical Review B 96, 024426 (2017)
[5] [SLaSi spin–lattice simulations package]
