Bogolyubov Kyiv Conference "Problems of Theoretical and Mathematical Physics"

24 Sep 2024, 09:00 → 26 Sep 2024, 18:00 Europe/Kiev

322 (Bogolyubov Institute for Theoretical Physics (Section 1-4), Institute of Mathematics (Section 5))

The Conference is dedicated to the 115th anniversary of the outstanding theoretician in physics and mathematics Mykola Bogolyubov (21.08.1909-13.02.1992)

Conference topics

1. HIGH ENERGY PHYSICS AND NUCLEAR MATTER 
2. STATISTICAL PHYSICS AND KINETIC THEORY
3. ASTROPHYSICS AND COSMOLOGY
4. CONDENSED MATTER PHYSICS
5. MATHEMATICS

Organizing Committee

Chairman

Anatoly  Zagorodny

Scientific Secretary

Ivan Starodub (Sections 1-4), Maryna Nesterenko (Section 5)

Mykola  Azarenkov, Larissa  Brizhik, Taras  Bryk, Alexander  Chalyi, Alexandre  Gavrilik, Viktor  Gerasimenko, Mark  Gorenstein, Valery  Gusynin, Yuri  Izotov, Vyacheslav  Kochelap, Bohdan  Lev, Vadym  Loktev, Ihor  Mryglod, Leonid  Pastur, Sergiy  Perepelytsya, Elmar  Petrov, Yuriy  Slyusarenko, Alexander  Timokha, Andrey  Varlamov, Ihor  Yukhnovskii, Volodymyr  Zasenko

Local Organizing Committee

Musfer  Adzhymambetov, Volodymyr  Dailidonis, Mykola  Glushko

Participants need to present their reports offline in Kyiv.

Venue: Kyiv , Metrolohichna str., 14-b (Map)

Listeners will be able to connect online, the event will be streamed on the YouTube channel of the Institute (access link).

 

Bogolyubov Kyiv Conference Program.pdf

Bogoyubov_Conf-2024.pdf

Poster Session Program.pdf

Program Sec5 Bogolubov 2024.pdf

Tuesday, 24 September

10:00 → 13:30 Morning session 1

10:00 Conference opening

Speaker: Anatoly Zagorodny (NAS of Ukraine)

10:20 Critical point in system of interacting bosons

A system of bosons studied within the mean field framework has two fascinating phenomena: a liquid-gas first order phase transition and Bose-Einstein condensation. Interplay between these two phenomena is being investigated. Depending on the mean-field potential parameters one can observe two types of critical points (CP), called ”Boltzmann” and ”Bose”, that belong to different universality classes with distinct sets of critical exponents. As examples of Bose and Boltzmann CPs pion and α matter are considered, respectively. In general, the phase diagram can have one of the CPs or both of them.

Speaker: Mark Gorenstein (Bogolyubov Institute for Theoretical Physics, National Academy of Sciences of Ukraine)

11:00 Reading Ernst Ising’s dissertation hundred years on

The Ising model is an archetype describing collective ordering processes. As such, it is widely known in physics and far beyond. Less known is the fact that the thesis defended by Ernst Ising 100 years ago under supervision of Wilhelm Lenz [1] contained not only the solution of what we call now the ‘classical 1D Ising model’ but also other problems. Some of these problems are the subject of this report [2,3]. In particular, I will discuss (i) a model proposed in 1922 by Walter Schottky and its relation to the Ising model [2]; (ii) the combinatorial method Ernst Ising used to calculate the partition function for a chain of elementary magnets [3]; (iii) the generalizations of the two-state model suggested in Ernst Ising’s thesis but not exposed in his paper [3]. The talk is a part of an ongoing project that aims to prepare a bilingual, commented edition of the doctoral thesis of Ernst Ising [4].

[1]. Beitrag zur Theorie des Ferro- und Paramagnetismus. Dissertation zur Erlangung der Doktorwürde der Mathematisch–Naturwissenschaftlichen Fakultät der Hamburgischen Universität vorgelegt von Ernst Ising aus Bochum. Hamburg 1924; E. Ising. Beitrag zur Theorie des Ferromagnetismus. Zeitschr. f. Phys. 31 (1925) 253–258.

[2]. R. Folk, Yu.. Holovatch. Schottky's forgotten step to the Ising model. Eur. J. Phys. H 47 (2022) 9.

[3]. R. Folk, Yu. Holovatch. Ising's roots and the transfer-matrix eigenvalues. Entropy 26(6) (2024) 459.

[4]. B. Berche, R. Folk, Yu. Holovatch, R. Kenna, in preparation

Speaker: Yurij Holovatch (ICMP NASU, Lviv)

11:40 Properties of multi-qubit states representing directed graphs and their studies with quantum programming

We analyze multi-qubit states that can be represented using directed graphs G(V,E). We focus on the geometric properties of these states, namely on curvature and torsion [1]. It has been found that the curvature of quantum states is determined by the sum of the weighted degrees of nodes in graphs where the weights in G(V,E) are raised to the second and fourth powers [2]. Additionally, curvature depends on the sum of the products of the weights of edges that form squares within the graph G(V,E). The torsion, on the other hand, is connected to the sum of the products of the weights of edges that create triangles in the graph G(V,E). We have computed these geometric properties on IBM's quantum computer in the case of a quantum graph state corresponding to a chain [2].
We have also examined quantum states that represent directed networks. We calculated the entanglement of these states both analytically and by programming on AerSimulator. We identified relationships between the geometric measure of entanglement and the weights of incoming and outgoing arcs, the outdegree, and indegree of the vertex corresponding to the qubit in the graph [3].

[1] H. P. Laba, V. M. Tkachuk, Condens. Matter Phys. 20, 13003 (2017).
[2] Kh. P. Gnatenko Relation of curvature and torsion of weighted graph states with graph properties and its studies on a quantum computer, arXiv:2408.01511 (2024).
[3] Kh. P. Gnatenko Physics Letters A 521, 129815 (2024)

Speaker: Dr Khrystyna Gnatenko (Ivan Franko National University of Lviv)

12:00 Coffee break

12:30 To 190 years of the Wave of Translation and 50 years of the Davydov's soliton: Soliton dynamics in an oscillating magnetic field.

In this talk some less known facts of the discovery of the Wave of Translation will be discussed. A brief review of the advancement of the theory of Davydov's solitons will be given. New results on the study of the dynamics of the Davydov’s soliton [1] in an external oscillating in time magnetic field [2,3] will be reported.
It is shown that in the magnetic field, perpendicular to the molecular chain axis, soliton wave function is a superposition of the electron plane wave in the plane perpendicular to the molecular chain, and longitudinal component of the wave function which satisfies the modified Nonlinear Schroedinger equation which is solved using the perturbation method based on the inverse scattering transform. It is shown that soliton width and amplitude are constant, while its velocity and phase are oscillating in time functions with the frequency of the main harmonic determined by the magnetic field frequency. Account of the energy dissipation results in bounding soliton velocity from above due to the balance of the energy gain from the magnetic field, and its loss because of the radiation of linear sound waves and energy dissipation. Soliton radiation due to time-depending velocity is calculated and shown to be the most intensive at the resonant frequency of the magnetic field. It is concluded that such complex impact of time-depending magnetic fields on charge transport, provided by solitons, can affect functioning of the devices based on low-dimensional molecular systems. These results suggest the physical mechanism of the resonant therapeutic effects of oscillating magnetic fields as the resonant impact of the magnetic field on the charge transport processes provided by solitons in the redox processes [4,5].

Acknowledgement:
This work was supported by the fundamental scientific program 0122U000887 of the Department of Physics and Astronomy of the National Academy of Sciences of Ukraine. The author acknowledges the Simons Foundation (NY).

[1] A.S. Davydov, N.I. Kislukha. Solitary excitons in one-dimensional molecular chains. Phys. Stat. Sol. B (1973) 5 465. https://doi.org/10.1002/pssb.2220590212
[2] L. Brizhik. Davydov’s soliton in an external alternating magnetic field. arXiv:2402.09172v1 [cond-mat.soft] 14 Feb 2024.
[3] L. Brizhik. Dynamics of the Davydov's soliton in external oscillating magnetic field (Submitted to Chaos, Solitons and Fractals, 2024).
[4] L. Brizhik, E. Fermi, B. Zavan. Working principle of magnetic resonance therapy. http://arxiv.org/abs/1509.04475
[5] Electric, Magnetic, and Electromagnetic Fields in Biology and Medicine: From Mechanisms to Biomedical Applications: 2nd Edition. Bioengineering, Special Issue. (2024), 11.

Speaker: Larissa Brizhik (Boglyubov Institute fr Theoretical Physics)

12:50 Cubic-quintic interplay in the nonlinear Klein–Gordon model

The nonlinear Klein–Gordon (nKG) model,
$ \partial_{tt}\phi-c^{2}\partial_{xx}\phi+f(\phi)=0, $
is a universal model for describing the propagation of nonlinear waves in various physical media. For example, its stationary version describes the macroscopic wave function of the condensed phase (i.e., the order parameter) in the Landau theory of phase transitions. Noteworthy is also an application of the nKG model to modelling the spatially localised oscillating excitations of biological structures such as DNA chains. Here, the unknown real function $\phi$ is a characteristic of the wave field, $t$ is time, $x$ is coordinate, $c$ is the velocity parameter that deals with the speed of interaction propagation. The function $f$ is a nonlinear function of the wave field that describes the nonlinear response of the medium.

In this work, we are interested in the interplay between the cubic and quintic terms of the nonlinear response function, which we present as a truncated polynomial (corresponding to a $\phi^6$ field model),
$ f(\phi)=\alpha_1\phi+\alpha_{3}\phi^{3}+\alpha_{5}\phi^{5}. $
The real coefficient $\alpha_{1}$ describes the linear response of the medium. The real coefficients $\alpha_{3}$ and $\alpha_{5}$ represent the cubic and quintic nonlinearities, respectively.

By reducing the nKG model to an extended cubic-quintic nonlinear Schrödinger equation in Hamiltonian form, we demonstrate that the quintic nonlinearity has a profound effect on the stability of wave packets to long-wave modulations. When there is no quintic nonlinearity ($\phi^4$ field model), plain wave packets in such a system are known to be modulationally unstable for any carrier wave number in the case of negative coefficient at cubic nonlinearity. We show that such plain wave packets become modulationally stable for certain carrier wave numbers when the quintic nonlinearity becomes large enough. Such a stabilisation of the wave packet happens at certain critical ratio between the quintic and cubic coefficients of the nKG model.

This work proves that high-order nonlinear effects may play a decisive role in analysing physical phenomena in nonlinear models at certain conditions. This result may have practical implications for nonlinear media that exhibit the generation of higher harmonics and are characterised by a significant quintic nonlinearity (e.g, in polarisation). In particular, such conditions are met for ferroelectrics with first-order phase transition (e.g., BaTiO$_3$ crystals).

Publications:

1. Sedletsky Yu.V., Gandzha I.S. Hamiltonian form of extended cubic-quintic nonlinear Schrödinger equation in a nonlinear Klein-Gordon model. Phys. Rev. E 106, 064212 (2022). https://doi.org/10.1103/PhysRevE.106.064212

2. Sedletsky Yu.V., Gandzha I.S. Fifth-order nonlinear Schrödinger equation as Routhian reduction of the nonlinear Klein–Gordon model. Proc. R. Soc. A 479, 20230315 (2023). https://doi.org/10.1098/rspa.2023.0315

Speaker: Ivan Gandzha (Institute of Physics, National Academy of Sciences of Ukraine)

13-presentation.pdf

13:10 Entanglement of the diamond spin cluster

The entanglement of diamond spin systems in thermodynamic equilibrium has
been studied in various papers (for, example, [1, 2, 3, 4]). We focus on the evolution of entanglement in a diamond spin-1/2 cluster. This cluster consists of two central spins described by the anisotropic Heisenberg model, which interact with two side spins via an Ising interaction. The influence of the interaction coupling with the side spins on the entanglement of the central spins is investigated [5, 6]. It is demonstrated that the behavior of entanglement between the central spins can be controlled by choosing the appropriate value of this coupling. Additionally, we examine the influence of a bosonic bath on the entanglement of the central spins.

References
[1] I. Bose, A. Tribedi, Phys. Rev. A 72, 022314 (2005).
[2] A. Tribedi, S. Bose, Phys. Rev. A 74, 012314 (2006).
[3] O. Rojas, M. Rojas, S. M. de Souza, J. Torrico, J. Strecka, M. L. Lyra, Physica
A 486, 367 (2017).
[4] A. Ghannadan, KatarГңna Karl’ova, J. Strecka, Magnetochemistry 8, 11
(2022).
[5] A. R. Kuzmak, J. Phys. A 56, 165302 (2023).
[6] A. R. Kuzmak, Ann. Phys. (NY) 455, 169397 (2023).

Speaker: Dr Andrij Kuzmak (Professor Ivan Vakarchuk Department for Theoretical Physics, Ivan Franko National University of Lviv)

13:30 → 14:30 Lunch

14:30 → 16:10 Afternoon Session 1

14:30 Methods of Neutron Optics fof Studying Physical Properties of Liquids

This presentation is aimed at using neutron optics methods to study the physical properties of bulk and confined liquids. To achieve this goal, the defining idea of M.M. Bogolyubov regarding the hierarchy of relaxation times and the sequential description of the dynamic evolution of condensed systems was used [1]. The following results were obtained by the methods of neutron optics [2-6], which apply the Schrödinger equation for the neutron wave function and the Fermi potential depending on the local numerical value of the density of nuclei [2]:
1. For bulk liquids, the singular behavior of the temperature derivative for the diameter of the neutron refractive index (NRI) is theoretically predicted, the main reason for which is a violation of the Polyakov conformal invariance hypothesis on the coexistence curve of a real liquid-vapor system.
2. Due to the spatial inhomogeneity of the bulk fluid near the critical state in the external gravitational field (see, for example, [7,8]), the appearance of a uniaxial ellipsoid of the NRI has been proven (by analogy with the ellipsoid of wave normals in crystal optics). The parameters of such an ellipsoid were determined for a cylindrical volume of liquid with a radius significantly larger than the correlation length of density fluctuations. On the axis of such a cylindrical sample, the uniaxial NRI ellipsoid becomes the NRI sphere.
3. Different signs of the coherent scattering length of the components of the solution of liquids predict the phenomenon of zero refraction of the neutron beam, which resembles the zero optical activity of a racemic mixture. Theoretical calculations established that for a binary solution of ethane and carbon dioxide, the phenomenon of zero refraction of the neutron beam should take place in the solution of [6].
4. It was theoretically established that the temperature dependence of the peak width of quasi-elastic scattering of slow neutrons is quantitatively confirmed by experimental results for confined supercooled water with spatial dimension d = 2 near its lower critical temperature T = 2280С [9].
5. Using Mandelbrot's formula [10] for the fractal dimension, it was proved that the dependence of the cross section of the elastic neutron scattering, being proportional to the random mean-square fluctuation of the number density of nuclei, on linear sizes of a confined liquid volume is determined by a new critical index, which is equal to the fractal dimension. For systems that belong to the universality class of the Ising model in a magnetic field, the fractal dimension values are 1.875 and 2.482, respectively, for spatial dimensions d = 2 and d = 3 [11].
6. It has been proven that the method of quasi-elastic neutron scattering [4,6] makes it possible to create a reliable basis for new diagnostic tests of the carcinogenesis process based on the established correlation between the self-diffusion coefficient of water molecules in aqueous suspensions of plasma membranes and the sensitivity of different groups of tissues to anticancer drugs [12]. Another biomedical application of neutron optics methods is the calculation of NRI and refraction of a neutron beam in an aqueous suspension of proteins and lipids.

1. М.М. Bogolyubov. Problems of Dynamic Theory in Statistical Physics. Naukova Dumka, Kyiv, 1970
2. Enrico Fermi. Collected Paper: (Note e memorie), v.1. Italy 1921-1938; v.2. United States 1939-1954; University of Chicago Press, Chicago, 1964.
3. I.M. Frank, Neutron optics and ultracold neutrons, Phys. Sci. Advances 161(11): 109-127, 1991.
4. L.A. Bulavin, K.O. Chalyy. Neutron Optics of Mesoscale Liquids. Naukova Dumka, Kyiv, 2006.
5. V.I. Sygakov, О.V. Chalyi, L.М. Chernenko. Critical neutron opalescence in a heterogeneous liquid. 1. Ukr. J. Phys. 35(7): 1036-1941, 1990; 2. Ukr. J. Phys. 36(9) 1355-1362, 1991.
6. A.V. Chalyi, L.A. Bulavin, K.A. Chalyy. On the neutron optics of liquids. J. Mol. Liquids 383: 121979, 2023.
7. M.E. Fisher. The theory of critical point singularities. In M.S. Green (Ed.) Critical Phenomena. Intern. School Phys. “Enrico Fermi”, Acad. Press, New York, 1971.
8. K.A. Chalyy, K. Hamano, A.V. Chalyi. Correlating properties of a simple liquid at criticality in a reduced geometry. J. Mol. Liquids 92 (1-2) 153-164, 2001.
9. A.V. Chalyi. Dynamic anomalies in confined supercooled water and bulk fluids. In L.A. Bulavin and A.V. Chalyi (Eds.) Modern Problems of Molecular Physics, Springer, 253-290, 2018.
10. B. Mandelbrot. The Fractal Geometry of Nature. W.H. Freeman and Company, New York, 1982.
11. A.V. Chalyi. Effective fractal dimension at 2d – 3d crossover. Fractal and Fractional 6: 739-750, 2022.
12. L.A. Bulavin, V.F. Chekhun, O.A, Vasilkevych, V.I. Kovalchuk, V.T. Krotenko, V.I. Slisenko, V.P. Tryndyak, K.O. Chalyy. Neutron studies of self-diffusion of water molecules in plasma membranes. J. Phys. Studies 8(4):334-337, 2004.

Speaker: Prof. O. V. Chalyi (Department of Medical and Biological Physics and Informatics, O. O. Bogomolets National Medical University, Kyiv, Ukraine)

15:10 Effects of metallic and molecular counterions in structural dynamics of the DNA double helix

The structure of the DNA double helix is stabilized by water molecules and positively charged metallic or molecular ions, which form an ion-hydration shell around the macromolecule. The ions neutralize the negatively charged phosphate groups of the DNA backbone and thus act as counterions. Despite the extensive number of experimental and theoretical studies, the specific effects of counterions on the structural dynamics of the DNA double helix and its ion-hydration shell remain incompletely understood. This contribution will overview the most recent findings on this topic based on molecular dynamics simulation results. Specifically, the effects of hydration of Li$^+$, Na$^+$, K$^+$, Rb$^+$, Cs$^+$ and Mg$^{2+}$ counterions localized in different regions of the DNA macromolecule will be discussed, along with the interplay of water molecules around the ions and within the hydration shell of the double helix [1,2]. In the case of molecular ions, the role of conformational effects of flexible polyamines (putrescine$^{2+}$, spermidine$^{3+}$, and spermine$^{4+}$) for the interaction with the DNA double helix and the formation of stable DNA-DNA contacts will be described [3-6]. The results will be discussed in the context of understanding the physical mechanisms behind DNA's biological functioning and the development of DNA-based materials for nanotechnological applications.

[1] Perepelytsya, S. J. Mol. Model. 2018, 24 (7), 171. https://doi.org/10.1007/s00894-018-3704-x.

[2] Perepelytsya, S. M. Ukr. J. Phys. 2020, 65 (6), 510. https://doi.org/10.15407/ujpe65.6.510.

[3] Perepelytsya, S.; Uličný, J.; Laaksonen, A.; Mocci, F. Nucleic Acids Res. 2019, 47 (12), 6084–6097. https://doi.org/10.1093/nar/gkz434.

[4] Mocci, F.; Laaksonen, A.; Engelbrecht, L.; Vasiliu, T.; Perepelytsya, S. In Soft Matter Systems for Biomedical Applications. Springer Proceedings in Physics, vol 266; Springer, Cham., 2022; pp 163–192. https://doi.org/10.1007/978-3-030-80924-9_6.

[5] Vasiliu, T.; Mocci, F.; Laaksonen, A.; Engelbrecht, L. D. V.; Perepelytsya, S. M. Front. Chem. 2022, 10 (February), 836994. https://doi.org/10.3389/fchem.2022.836994.

[6] Perepelytsya, S.; Vasiliu, T.; Laaksonen, A.; Engelbrecht, L. D. V.; Mocci, F. Low Temperature Physics 2024, 50 (3), 204–214. https://doi.org/10.1063/10.0024969.

Speaker: Sergiy Perepelytsya (Bogolyubov Institute for Theoretical Physics of the NAS of Ukraine)

15:30 General hydrodynamic approach for a cold Bose gas

The aim of this paper is to derive the hydrodynamics for a cold Bose gas from the microscopic platform based on the many-body Schr¨odinger equation and general assumptions of the hydrodynamic approach (HA) applicable to any dimension. We develop a general HA for a cold spatially inhomogeneous Bose gas assuming two different temporal and spatial scales and obtain the energy as a functional of both fast inner quantum mode and slow macroscopic mode. The equations governing the fast and slow modes are obtained from this functional by their independent variations. The fast mode is the wave function in the stationary state at local density which can be ground, excited with a nonzero atom momenta, or a superposition of more than one states. The energy eigenvalue (or expectation value) of this local wave function universally enters the hydrodynamic equation for the slow mode in the form of the local chemical potential which incorporates the inner local momentum. For zero inner momenta and particular choices of this eigenvalue as a function of gas density, this equation reduces to the known equations based on the local density approximation. If however the inner momenta are nonzero, the equation includes the interaction between these momenta and the slow mode velocity. Relation between this general HA and the standard local density approximation is elaborated. Two effects of the local momenta and their density dependence on the soliton solutions are demonstrated.
(To appear in the Physical Review A, arXiv:2408.12363v1).

Speaker: Victor Pergamenshchik (Institute of Physics, NANU, Kyiv, Ukraine & Center for Theoretical Physics, PAN, Warsaw, Poland)

15:50 Coffee break

16:10 → 18:50 Poster Session

16:10 On the solution of the problem of the cosmological constant

Calculation of the vacuum energy density in quantum field theory gives a value $10^{122}$ times higher than the observed one, and many proposed approaches have not solved this problem and have not calculated its real value. However, the application of the microscopic theory of superconductivity to the description of the physical vacuum on the Planck scale made it possible to solve the problem of the cosmological constant and obtain a formula for the observed vacuum density or dark energy. Its numerical value is $6.09 \cdot 10^{-30} g/cm^3$, and it is in complete agreement with observations, since the experimental value is $(6.03 ± 0.13) \cdot 10^{-30} g/cm^3$ (J. Prat, C. Hogan, C. Chang, J. Frieman, 2022).
The cosmological model with superconductivity (CMS), proposed by the author, also implies a description of the earliest stage of the Universe evolution preceding the inflation stage. It describes the formation of the inflaton field as a special condensate of primordial fermions with the Planck mass, followed by the inflationary expansion of the early Universe. The current expansion of the Universe and its evolution are described as an ongoing second-order phase transition, and the flow of physical cosmological time is a consequence of processes occurring on Planck scales. The value of the Hubble parameter $H_0=69.76 \ km \cdot s^{-1}Mpc^{-1}$ calculated in CMS corresponds to the average value for most values of this parameter obtained by different methods. CMS also describes black holes as a quantum condensate of primary fermions with Planck mass.

References:

1. Weinberg, S., “The cosmological constant problem”, Reviews of Modern Physics, vol. 61, no. 1, APS, pp. 1–23, 1989. doi:10.1103/RevModPhys.61.1.
2. Bukalov, A. V., “The Solution of the Cosmological Constant Problem and the Formation of the Space-Time Continuum”, Odessa Astronomical Publications, vol. 29, p. 42, 2016. doi:10.18524/1810-4215.2016.29.84962.
3. Pitaevskii, L. P., Lifshitz, E. M. Statistical Physics Part 2 (1980).
4. Fomin, P. I., “Zero cosmological constant and Planck scales phenomenology”, Proc. of the Fourth Seminar on Quantum Gravity, May 25–29, Moskow / Ed. by M.A.Markov. — Singapore: World Scientific, 1988. — P. 813.
5. Fomin, P. I., “On the crystal-like structure of physical vacuum at Planck distances”, Problems of physical kinetics and solid state physics. Kyiv: Naukova dumka, 1990. — P. 387–398.
6. Bukalov, A. V., “On solving the problem of the cosmological constant”, Proceedings of 12-th Odessa International Astronomical Gamow Conference-School “Astronomy and Beyond: Astrophysics, Cosmology and Gravitation, Cosmomicrophysics, Radio-astronomy and Astrobiology” 20-26 August, 2012, Odessa, Ukraine. — P. 28.
7. Prat, J., Hogan, C., Chang, C., and Frieman, J., “Vacuum energy density measured from cosmological data”, Journal of Cosmology and Astroparticle Physics, vol. 2022, no. 6, IOP, 2022. doi:10.1088/1475-7516/2022/06/015. arXiv:2111.08151.

Speaker: Oleksandr Bukalov (Centre for Physical and Space Research, International Institute of Socionics)

24_Bukalov Constant.pptx

24_uk_Bukalov Constant.pdf

Poster.pdf

16:15 Collapse mitigation in a socioeconomic system under a systemic shock

Systemic shocks inevitably lead to negative socioeconomic outcomes. The COVID-19 pandemic and the war in Ukraine are the prominent examples of such systemic shocks. Shock-initiated spreading processes often have a domino effect on both the social and economic levels. The war in Ukraine, despite its devastating effect on the Ukraine’s society and economy, has not led to the full collapse, against all odds. In this work, we make an attempt to provide at least a qualitative illustration of the mechanisms governing the dynamics of a socioeconomic system in the state of collapse from the viewpoint of statistical physics. Surprisingly, we uncover common principles that allow the overall collapsing scenario to be mitigated, with the system’s dynamics stabilized.

We consider a response of a socioeconomic system to a systemic shock in a group of economic agents with limited economic resource. To this end, we exploit a simple two-level model of active and passive economic agents with mutual negative feedback between the number of active agents and collective resource acquisition [1]. In this case, economic resource is associated with the average amount of money or income per economic agent and formally corresponds to the effective market temperature, with the income distribution of economic agents obeying the Boltzmann–Gibbs statistics [2]. The coupling between the spreading process and resource in such a system is supposed to be of activation type, with the transition rate between the passive and active populations governed by the activation mechanism (Arrhenius-like law). A characteristic level of resource consumption is associated with activation energy (e.g., corresponding to the minimum level of resource consumption in our particular case).

We show that the phase portrait of the system features a collapse phase, in addition to the shock-free and post-shock phases. The shock intensified by the increasing resource deficit can ultimately drive the system to a collapse at nonzero activation energy because of limited resource – the effect opposite to thermal explosion. In this case, the system can no longer stabilize and return to the stable shock-free state or a poorer post-shock state. We demonstrate that there exists a certain critical point at which the system collapses at any initial conditions. Moreover, social regulations in the case of low economic resource can have a negative effect and provoke the system’s collapse. On the other hand, there are simple external measures that can protect the system against the collapse, which make the focus of our investigation. We demonstrate that the system’s collapse can partially be mitigated by external subsidies meaning constant resource inflow from some external source or by means of debt interpreted as a negative resource.

It is interesting that a two-level model considered here formally describes the dynamics of cooling of a system of agents due to shock-induced transitions between two discrete inner states of agents. In this case, the crisis state of the financial market can be associated with a Bose condensate-like state at low market temperature [3]. A more complex multi-level system of interacting agents as well as different interacting social groups can also be considered [4].

[1] Gandzha I.S., Kliushnichenko O.V., Lukyanets S.P. A toy model for the epidemic-driven collapse in a system with limited economic resource. Eur. Phys. J. B 94, 90 (2021).
https://doi.org/10.1140/epjb/s10051-021-00099-7; https://arxiv.org/abs/2012.12113
[2] Yakovenko V.M., Rosser J.B., Jr. Colloquium: Statistical mechanics of money, wealth, and income. Rev. Mod. Phys. 81, 1703 (2009). https://doi.org/10.1103/RevModPhys.81.1703
[3] Kusmartsev F.V. Statistical mechanics of economics I. Phys. Lett. A 375, 966 (2011).
https://doi.org/10.1016/j.physleta.2011.01.003
[4] Gandzha I.S., Kliushnichenko O.V., Lukyanets S.P. Modeling and controlling the spread of epidemic with various social and economic scenarios. Chaos, Solitons & Fractals 148, 111046 (2021).
https://doi.org/10.1016/j.chaos.2021.111046

Speaker: Sergey Lukyanets (Institute of Physics, National Academy of Sciences of Ukraine)

poster_2_Lukyanets_A0.pdf

16:20 Graph Structural Complexity

Introduced the quantitative measure of the structural complexity of the graph (complex network, etc.) based on a procedure similar to the renormalization process, considering the difference between actual and averaged graph structures on different scales. The proposed concept of the graph structural complexity corresponds to qualitative comprehension of the complexity. The proposed measure can be obtained for the weighted graphs also.
The structural complexities for various graph types were found – the deterministic infinite and finite size graphs, artificial graphs of different natures including percolation structures, and the time series of cardiac rhythms mapped to complex networks using the parametric visibility graph algorithm. The latter reaches a maximum near the formation of a giant component in the graph or at the percolation threshold for 2D and 3D square lattices when a giant cluster having a fractal structure has emerged. Therefore, the graph structural complexity allows us to detect and study the processes similar to a second-order phase transition in complex networks.
A new node centrality index, characterizing the structural complexity of a certain node within the graph structure is introduced also, it can serve as a good auxiliary or generalization to the local clustering coefficient. Such an index provides another new ranking manner for the graph nodes.
Being an easily computable measure, the graph structural complexity might help to reveal different features of complex systems and processes of the real world.

Speaker: Prof. Andrei Snarskii (The National Technical University of Ukraine "Igor Sikorsky Kyiv Polytechnic Institute", Dep. of General Physics)

16:25 Lattice models of ionic liquids in conducting slit nanoconfinement

Confined ionic liquids exhibiting exciting physics are essential in modern technologies. The narrow conducting confinements cause exponential screening of the electrostatic interactions between ions, allowing the development of models with short-range interactions that can provide analytical insights into the charge storage mechanisms. In this contribution, we present a lattice model for ionic liquids confined in ultranarrow slit-shaped pores admitting a single layer of ions. In the case of next-nearest interactions, it can be mapped onto the well-known three-state Blume-Capel model, which obeys an analytical solution within the Bethe-lattice approximation [1]. Analyzing phase behavior and pore charging in terms of pore ionophilicity, interionic interactions, and applied potential difference, we obtained a phase diagram comprising the lines of first- and second-order, direct and re-entrant phase transitions, manifested by singularities in the capacitance-voltage dependence [2]. These analytical results are corroborated by lattice Monte Carlo simulations [3]. However, it is known that, at least in the quasi-one-dimensional case of single-file pores, the results of the lattice model with short-range interactions differ even qualitatively from the exact results of the corresponding continuous model [4]. We will discuss possible ways to improve the lattice model by considering further interactions and analyzing changes in the phase diagram depending on the interaction parameters.

This research is supported by bilatheral project № M/72-2024 between Ministry of Education and Science of Ukraine and Polish National Agency for Academic Exchange (NAWA) as well as U. S. Department of Energy (DOE), Office of Science, Basic Energy Sciences, Materials Science and Engineering Division, under Award No. DE–SC0013599 (Subaward No. UTAUS-SUB00000795)

[1] M. Dudka, S. Kondrat, A.A. Kornyshev, G. Oshanin, J. Phys.: Condens. Matter 28, 464007 (2016).
[2] M. Dudka, S. Kondrat, O. Benichou, A. A. Kornyshev, G. Oshanin, J. Chem. Phys. 151, 184105 (2019).
[3] Ya. Groda, M. Dudka, A.A. Kornyshev, G. Oshanin, S. Kondrat, J. Phys. Chem. C 125, 4968 (2021)
[4] T. Verkholyak, A.Kuzmak, S. Kondrat, J. Chem. Phys. 155, 174112 (2021)

Speaker: Maxym Dudka

16:30 Subensembles of magnetized particles in random electric fields

Transport processes of a passive scalar in random velocity fields are observed in plasma systems, atmosphere, oceanic currents, etc. The task of the theoretical description is to reproduce the temporal evolution of an ensemble of particles moving in such a field based on the known statistical characteristics of the velocity or force fields. The most known example is Brownian motion, the feature of which is the presence of two time scales. That is, the time of collisions, or the time of correlations of random fields, is much shorter than the time of system, or the particle distribution function, evolution. Then, as is known, the mean squared displacement of the particles, or the second moment of the distribution function, is proportional to the system evolution time. The distribution of particles, which at the initial moment of time were concentrated at the origin of the coordinates, preserves the Gaussian shape, which evolves according to the mean squared displacement, and the particle diffusion coefficient in such fields is a constant value.
More complicated and more interesting is the transport of particles in random fields, the correlation time of which is not small compared to the time of evolution of the system. An example of such a system is charged particles drifting in a random electric field across a constant magnetic field. The equations of motion become statistically nonlinear, and the evolution of dispersion from a short initial ballistic regime, namely quadratic dependence on time, changes asymptotically to a fractional power law. Accordingly, the distribution of particles is not Gaussian, and the diffusion coefficient changes over time.
The feature of such a system is that the two-dimensional drift of particles occurs along equipotential lines or streamlines. The presence of such an integral of motion allows for dividing the complete ensemble of particles into separate groups named subensembles, which are concentrated near streamlines with a certain value of potential. Observation of subensembles allows a better understanding of how the transport occurs as a whole. In this work, the behavior of the moments of the particle distribution function was studied using simulation for subensembles with the same initial value of the random potential, in particular, the mean squared displacement and excess kurtosis were calculated. It is shown that in each subensemble there are particles that travel far from the initial position and that remain close to it. The distribution of the displacement of particles depending on the initial value of the potential was found, and the average displacements and velocities for the sub-ensembles were calculated. It was found that the mean square displacement of the entire ensemble of particles is formed from the partial contributions. The obtained statistical characteristics of particle motion are useful for the verification of analytical models.

Speaker: Oleksandr Cherniak (Bogolyubov Institute for Theoretical Physics)

16:35 Spin-boson description of the temporal behavior of the dynamical system with time-dependent coupling to the environment

This work shows how a kinetic process is formed in a dynamic system that is in a non-stationary coupling with the environment. It is assumed that the environment has a large number of degrees of freedom and therefore transitions in a dynamic system do not change the state of the environment. However, due to the openness of a dynamic system, the environment is capable of modifying both the states of the system and its energy levels. We are considering a quantum dynamic system, where the exchange of energy between the system and the environment is carried out through vibrational quanta (phonons). Using the method of nonequilibrium statistical mechanics, kinetic equations are obtained that describe the time evolution of the density matrix of a dynamic system under conditions of strong (polaron) coupling with vibrational modes of both the environment and the system. The difference from a similar type of research is that the coupling between the electronic states of the system and its vibration states is assumed to be time-dependent. We proposed a unitary-transformation, which made it possible to take into account this non-stationary coupling directly in the operator responsible for transitions between states of the system. This opened up the possibility of using the perturbation method to derive the master equation for the probabilities of occupying system states. As an example of the application of non-stationary polaron transformation, the kinetics of establishing the probabilities of occupation of electronic states of an open TLS is considered.

Speaker: Yevgen Shevchenko (Bogolyubov Institute for Theoretical Physics, National Academy of Sciences of Ukraine)

16:40 Nonequilibrium protection effect and spatial localization of noise-induced fluctuations: gas flow scattering on partially penetrable obstacle

The scattering of gas flow on an obstacle can lead to the formation of nonequilibrium steady states (NESS), such as stationary obstacle wakes. These systems may undergo nonequilibrium phase transitions, resulting in the emergence of nonlinear steady-state gas structures under critical conditions. One notable example is the formation of a stratum-like, or two-domain, gas structure ahead of the obstacle due to the blockade effect in the gas [1-5]. This structure can be interpreted as the growth of a dense gas phase nucleus near the obstacle, which acts as a nucleation center.

In our study, we focus on a quasi-one-dimensional driven lattice gas doped with static impurities within a narrow channel with ring topology [1]. The obstacle is modeled as a transverse channel cell partially occupied by impurity particles, and the system is driven by a nonconservative field. We utilize a combination of the local equilibrium approach and mean-field approximation to describe the NESSs and gas fluctuations near them.

Our findings reveal that this nonequilibrium transition is associated with the emergence of a local invariant. Specifically, the state of the obstacle behaves as a local first integral (or adiabatic invariant), becoming insensitive to fluctuations in the gas and the external driving noise.

Below the transition, the gas flow is scattered by the impurity, the structural defect of the lattice. Above the transition, the gas flow is scattered by the gas domain wall, the defect of the gas density distribution. This leads to the protection effect of the obstacle state against gas fluctuations, manifesting as a strong localization of fluctuations near the topological defect (domain wall) and their complete suppression at the obstacle. Additionally, gas fluctuations demonstrate strong anti-correlated behavior at the left and right sides of the impurity. These effects are similar to the skin effect and edge-edge correlation effect in non-Hermitian systems [6].

References:

[1] S.P. Lukyanets, O.V. Kliushnichenko, Phys. Rev. E 109, 054103 (2024). https://doi.org/10.1103/PhysRevE.109.054103
[2] S. A. Janowski and J. L. Lebowitz, Phys. Rev. A 45, 618 (1992).
[3] K. Mallick, Physica A 418, 17 (2015). https://doi.org/10.1016/j.physa.2014.07.046
[4] A. Chumak and A. Tarasenko, Surf. Sci. 91, 694 (1980); A. A. Tarasenko, P. M. Tomchuk, and A. A. Chumak, Fluctuations in the Bulk and on the Surface of Solids (Naukova Dumka, Kyiv, 1992).
[5] D. N. Zubarev, Nonequilibrium Statistical Thermodynamics (Plenum Press, New York, 1974).
[6] S. Shankar, A. Souslov, M.J. Bowick, M.C. Marchetti, and V. Vitelli, Nat. Rev. Phys. 4, 380 (2022). https://doi.org/10.1038/s42254-022-00445-3

Speaker: Oleksandr Kliushnichenko (Institute of Physics, National Academy of Sciences of Ukraine)

Bogolyubov_Kyiv_Conf___2024.pdf

16:45 The development of Bogolyubov reduced description method in the application to spin and quasispin systems

The development of Bogolyubov reduced description method
in the application to spin and quasispin systems
Sokolovsky A. I., Lyagushyn S. F.
Oles Honchar Dnipro National University
The reduced description method (RDM) is based on the Bogolyubov’s idea that at large time the non-equilibrium state evolution of a macroscopic system can be described with the limited number of parameters. The way to the right choice of such parameters and constructing the equations of time evolution for them was opened by the works of Kharkiv school in statistical physics [1]. Since early 2000-ies the authors deal with applying the proposed technique to Dicke superradiance – the unique phenomenon of emitter system self-organization in the process of reaching the equilibrium state from excited one. We are interested in a more detailed picture of correlation development both in emitter and field subsystems. The problem of correlator decoupling which arises in the Bogolyubov method of boson variable elimination [2], seems worthy of attention. In RDM, including the binary correlation functions into the set of reduced description parameters (RDPs) results in the necessity of calculating the averages with quasi-equilibrium Hamiltonians where such new parameters are present. Usually, two-level electromagnetic emitters are described using the quasispin operators constructed with Pauli matrices. While considering the acoustic superradiance, spin and phonon operators are necessary for the Hamiltonian construction. The operator forms prove to be the same for boson fields of different nature. Thus, we face the problem of averaging in the case when the exponential statistical operator includes a quadratic form of spin operators in the exponent that cannot be done exactly.
In our recent papers [3, 4], a new approach consisting of introducing additional small parameter in the theory of relaxation processes in spin systems has been proposed. While the spin-boson interaction constant is a customary small parameter in the specified theory, we put forward the idea of accounting for small deviations of correlation functions taken as RDPs from their values calculated in the picture with the only RDP describing the state of a spin (quasispin) system – the excitation degree of the emitter subsystem ${{\eta }_{1}}$ (${{s}^{z}}=\sum\limits_{1\le i\le N}{s_{i}^{z}}$ in usual designations). Restricting ourselves with the concentrated Dicke model, we can use the known equation for ${{s}^{z}}$ possessing the integral of motion including the binary correlation function $\left\langle {{{\hat{s}}}^{+}}{{{\hat{s}}}^{-}} \right\rangle $. In the theory of superradiance using $\left\langle {{{\hat{s}}}^{+}}{{{\hat{s}}}^{-}} \right\rangle $ as an independent RDP ${{\eta }_{2}}$ (${{\hat{\eta }}_{2}}={{\hat{s}}^{+}}{{\hat{s}}^{-}}$), we construct the quasi-equilibrium statistical operator of RDM ${{\rho }_{q}}={{e}^{\Omega -{{Z}_{1}}{{{\hat{\eta }}}_{1}}-{{Z}_{2}}{{{\hat{\eta }}}_{2}}}}$ implying the condition of smallness of the deviation $\delta {{\eta }_{2}}=Sp({{\rho }_{q}}-\rho _{q}^{0}){{\hat{\eta }}_{2}}$, i.e. difference between correlation function obtained with such operator and those of RDM model with ${{\eta }_{1}}$ only $\rho _{q}^{0}={{e}^{{{\Omega }^{0}}-Z_{1}^{0}{{{\hat{\eta }}}_{1}}}}$. We use $\delta {{\eta }_{2}}$ as a new small parameter of the order $\mu $ and the statistical operator ${{\rho }_{q}}$ can be expressed via $\rho _{q}^{0}$ in the form of μ power expansion. Thus, we obtain expressions for spin average deviations with an error up to $\mu^{3}$ and evolution equations for ${{\eta }_{1}}$, ${{\eta }_{2}}$, and boson RDPs ${{n}_{k}}$. The solved problem relates to cumbersome calculations but only averages with linear forms of spin operators and quadratic forms of boson operators are needed. The technique of averaging for spin operators was improved in the framework of our activities. The results are applicable for different versions of Dicke model and Wagner model of acoustic superradiance.
1. Akhiezer, A. I. Methods of Statistical Physics / A. I. Akhiezer, S. V. Peletminskii. – Oxford: Pergamon Press, 1981. – 450 p.
2. Bogolyubov, N. N. (Jr.) Sverkhizlucheniye / N. N. Bogolyubov (Jr.), A. S. Shumovsky. – Dubna: JINR, 1987, JINR publication P17-87-176. – 88 p.
3. Lyagushyn, S. F. Taking into account the influence of correlations on the system dynamics in the reduced description method / S. F. Lyagushyn, A. I. Sokolovsky // Journal of Physics and Electronics. –2023 – Vol. 31(1). – P. 7 – 17. https://doi.org/10.15421/332302
4. Sokolovsky, A. I. Dynamics of a system of two-level emitters in the Dicke model taking into account small correlations between them / A. I. Sokolovsky, S. F. Lyagushyn // Journal of Physics and Electronics. –2023 – Vol. 31(2). – P. 88 – 110. https://doi.org/10.15421/332326

Speaker: Serhiy Lyagushyn (Oles Honchar Dnipro National University)

16:50 AdS/CFT correspondence and and classification of Kaluza-Klein modes within the supergroup

Within the framework of AdS/CFT correspondence we considered large N limits of conformal field theories in d dimensions which described in terms of supergravity on the product of AdS space with a compact manifold. An important example of such correspondence is equivalence between N = 4 super Yang-Mills theory in four dimensions and Type IIB superstring theory on $AdS_5 × S^5$ [1]. The confirmation of this correspondence comes from the fact that the Kaluza-Klein modes of type IIB supergravity on $AdS_5 × S^5$ coincide with the chiral operators of N = 4 super Yang-Mills theory in four dimensions. Moreover, to describe N = 4 super Yang-Mills theory in four dimensions, one should use low energy supergravity on $AdS_5$ and the infinite tower of massive Kaluza-Klein states on $AdS_5 × S^5$ [2]. The supersymmetry group of $AdS_5 × S^5$, is known to be the same as the superconformal group in 3+1 spacetime dimensions. So, the supersymmetries of Type IIB superstring theory on $AdS_5 × S^5$ and Yang-Mills theory in four dimensions are given by the same superconformal group SU(2,2|4). We presented the Kaluza-Klein masses and their multiplet classification corresponding to the superconformal group representations.

1. Edward Witten. Anti De Sitter Space And Holography. Adv.Theor.Math.Phys.2:253-291,1998.
2. Juan M. Maldacena. The Large N Limit of Superconformal Field Theories and Supergravity. Adv.Theor.Math.Phys.2:231-252,1998

Speaker: Dr Tetiana Obikhod (Institute for Nuclear Research NAS of Ukraine)

16:55 Spontaneous magnetization and effective interactions in QGP at high temperature

In quark-gluon plasma (QGP), at higher deconfinement temperatures $T \ge T_d$ the spontaneous generation of color magnetic fields, $b^3(T), b^8(T) \not = 0$ (3, 8 are color indexes), and usual magnetic field $b(T) \not = 0$ happens. Simultaneously, the Polyakov loop and/or algebraically related to it $A_0(T)$ condensate, which is solution to Yang-Mills imaginary time equations, are also created.
Usually, in analytic quantum field theory these effects are investigated independently of each other within the effective potentials having different mathematical structures.
The common generation of these condensates was detected in lattice Monte Carlo simulations.

Recently, with the new type two-loop effective potential, which generalizes the known integral representation for the Bernoulli polynomials and takes into consideration the magnetic background, this effect has been derived analytically.
The corresponding effective potential $W(T, b^3, A_0 )$ was investigated either in SU(2) gluodynamics or full QCD. The gauge fixing independence of it was proved within the Nielsen identity approach. The values of magnetic field strengths at different temperatures were calculated and the mechanism of stabilizing fields due to $A_0(T)$ condensate has been discovered. In the present review, we describe this important phenomenon in more details, as well as a number of specific effects happening due to vacuum polarization at this background. They could serve as the signals of the QGP creation in the heavy ion collision experiments.

Key words: spontaneous magnetization, high temperature, asymptotic freedom, effective potential, $A_0$ condensate, effective charge, effective vertexes.

Speaker: Prof. Volodymyr Skalozub (Oles Honchar Dnipro National University)

17:00 Constraints on the parameters of HNL and baryon asymmetry of the Universe

One of the simplest renormalizable extensions of the SM is the minimal neutrino extension of the Standard Model $\nu$MSM, proposed in 2005 [1, 2]. This modification introduces three righthanded neutrinos or heavy neutral leptons (HNL). The lightest sterile neutrino is identified as a dark matter particle. The other two sterile neutrinos are much heavier, with nearly identical masses, and are responsible for generating the baryon asymmetry observed in the Universe. The observable parameters of the $\nu$MSM Lagrangian are given in [3]
$$\begin{align} & S_{\alpha\beta} \equiv (F M^{-1\ast}M^{-1} F^\dagger)_{\alpha\beta} = \sum_I S^I_{\alpha\beta} = \sum_I F_{\alpha I}F^\dagger_{I \beta} M_I^{-2},\\ & R_{\alpha\beta} = \sum_I R^I_{\alpha\beta} = \sum_I S^I_{\alpha\beta}\ln\frac{M_I}{M_W} = \sum_I F_{\alpha I}F^\dagger_{I \beta} M_I^{-2} \ln\frac{M_I}{M_W}. \end{align}$$ In the $\nu$MSM framework, the lightest sterile neutrino, which serves as a long-lived dark matter particle, is undetectable in collider experiments. Therefore, we focus on a simplified scenario that extends the SM by incorporating only two heavy sterile neutrinos. A straightforward relationship has been derived between the experimentally observed quantities (the elements of the matrices Sαβ and Rαβ). This relationship holds for cases where active neutrinos have non-zero masses and where the masses of the heavy sterile neutrinos vary. $$\begin{equation} S_{\alpha \beta}\Bigl(M_1\ln \frac{M_2}{M_W}+M_2\ln \frac{M_1}{M_W}\Bigr)=R_{\alpha \beta}(M_1+M_2),\quad S_{\alpha \alpha} S_{\beta \beta} = |S_{\alpha \beta}|^2 \quad R_{\alpha \alpha} R_{\beta \beta} = |R_{\alpha \beta}|^2. \end{equation}$$ Building on the results of [1], we have translated the constraints on baryon asymmetry generation in the early Universe into observable parameters $S_{\alpha \beta}$ and $R_{\alpha \beta}$. We concluded that the actual values of elements of $\hat R$ and $\hat S$ matrices are many orders of magnitude less than existing experimental constraints. Results of our investigation are presented in detail in [4].
Acknowledgment. The work of V.G. and O.Kh. was supported by the National Research
Foundation of Ukraine under project No.2023.03/0149.

[1] T. Asaka and M. Shaposhnikov, Phys. Lett. B, 620, 17 (2005).
[2] S. Blanchet, T. Asaka and M. Shaposhnikov, 151 (2005).
[3] R. Coy and M. Frigerio, Phys. Rev. D 99, 095040 (2019).
[4] V. Gorkavenko, O. Khasai, O. Ruchayskiy, M. Tsarenkova, arXiv:2408.02107 [hep-ph].

Speaker: Oleksandr Khasai (Bogolyubov Institute for Theoretical Physics of the National Academy of Sciences of Ukraine)

17:05 Microscopic derivation of the generalixed Bohr Hamiltonian

The Bohr’s Hamiltonian is one of the main cornerstones of the nuclear structure theory. It was derived by Bohr [1], treating the nucleus as a liquid spherical drop with uniform density and sharp surface, performing quadrupole vibrations with small amplitude. During such oscillations at any moment of time the nucleus attains an ellipsoidal shape, retaining its volume constant due to small compressibility of the nuclear matter.
Following the microscopic theory [2], where the kinetic energy operator of the nucleus has been expressed in terms of the independent set of 3N collective variables, we constructed the collective Hamiltonian for nuclei with arbitrary deformation [3], which recovers the results of Bohr [1] at β << 1. First the classical kinetic energy T of N nucleons in the center-of-mass frame is expressed in terms of the Jacobi vectors ${\bf q}_i $, where $i=1, 2, …, n=N-1$. Then we introduce the rotating frame with axes ξ, η, ζ directed along the principal axes of the nuclear tensor of inertia. Its orientation is determined by the Euler angles φ, ϑ, ψ. In this case the off-diagonal elements of the inertia tensor vanish, so that
$ \sum_{i=1}^na_{i\xi}a_{i\eta}=\sum_{i=1}^na_{i\xi}a_{i\zeta}= \sum_{i=1}^na_{i\eta}a_{i\zeta}=0,$
where $a_{i\nu}$ denote the projections of of the Jacobi vectors on the axes frame ξ, η, ζ. We introduce an abstract Eucledian space with basis orthonormal vectors ${\bf e}_i $ and define there three vectors ${\bf A}_{\nu}$ with components $a_{i\nu}$ and lengths $ a_{\nu}$. The above consraint can be treated as an orthogonality condition for these vectors, while their lengths $a_1,\;a_2,\;a_3$ serve as three collective coordinates, specifying size and shape of the nucleus. It is natural to determine the remaining 3n-6 internal coordinates as any rotational variables, which describe orientation of three vectors in the n-dimensional hyperspace. For this aim we take the generalized Euler angles θjk, introduced by Vilenkin.
Following Bohr’s model [1], we demand that the vibrations and rotations only change a shape of the ellipsoidal nucleus keeping unchanged its volume, i.e., we demand that at arbitrary deformations the product of radii Rκ of the nuclear ellipsoid is related to the radius $R_0$ of the sphere with the same volume by $R_1R_2R_3=R_{03}$ at $R_0=const$. The radii, meeting this condition, we chose as [3] $R_{\kappa}=R_0{\cal E}_{\kappa}(\beta,\gamma)$, with ${\cal E }_{\kappa}(\beta,\gamma)=\exp\left[\tilde{\beta} \cos\left(\gamma-\frac{2\pi}{3}\kappa\right)\right]$ and $\tilde{\beta}=(5/4\pi)^{1/2}\beta$. When β<<1, the above expressions for Rκ coincide with well known ones and respectively our generalized parameters β, γ coincide with Bohr’s variables. Expressing the kinetic energy T in the suggested collective coordinates and then quantizing it, we derived the Hamiltonian, depending on the exactly determined inertia functions $b_{\lambda\lambda'}(\beta,\gamma)$, in contrast to existing in literature Hamiltonians, written ad hoc with unknown inertia parameters.
1. A. Bohr, Dan. Mat. Fys. Medd. 26, 14 (1952).
2. A. Ya. Dzyublik, V. I. Ovcharenko, A. I. Steshenko, and G. F. Filippov, Sov. J. Nucl. Phys. 15, 487 (1972).
3. A. Ya. Dzyublik, K. Starosta, Z. Yu., and T. Koike, Phys. Rev. C 110, 014325 (2024).

Speaker: Dr Alexey Dzyublik (Institute for Nuclear Research of NASU)

17:10 Polaronic model of the Giant Dielectric and Pyroelectric Responses of Ferroelectric Fine-Grained Ceramics

We described the anomalous temperature behavior of the giant dielectric response and losses using the core-shell model for ceramic grains and modified Maxwell-Wagner approach. We assume that core shells and grain boundaries, which contain high concentration of space charge carriers due to the presence of graphite inclusions in the inter-grain space, can effectively screen weakly conductive ferroelectric grain cores.
We considered several possible mechanisms, which can lead to the giant values of the relative dielectric permittivity accompanied by the very high values of dielectric losses in the strongly inhomogeneous ferroelectric-semiconducting ceramics.
The first mechanism is the effect of “geometric” capacitance, which could appear in the highly porous mixtures of the insulating and conducting inclusions. In this case the effective surface area of the capacitor could be much larger than the electrodes area, and the effective area could accumulate the space charge. Note that the geometric capacitance effect contribution could be verified by measuring the capacitance of the ceramic samples of different cutting angles, thickness, electrode area, frequency, and temperature.
The second mechanism is the Maxwell-Wagner effect [1], which could lead to the apparent enhancement of the dielectric response in the dielectric-semiconducting mixture in the presence of insulating polar grains, screening shells and conducive graphite inclusions. In principle all conductivity effects in the inhomogeneous media are strongly inter-wined and closely related with possible electric percolation effects. The possible roles and relative contributions of the different conductivity effects were considered with the help of the different theoretical models.
According to the effective media model proposed by Liu et al. [2], the one can consider two (or more) layers representing all grain cores, their screening shells and grain boundaries, graphite inclusions and inter-grain space in the Maxwell-Wagner approach. One of the “effective” layers corresponds to weakly-conductive grain cores, and the other corresponds to all stronger conductive regions (such as screening shells, grain boundaries and/or inter-grain space). The layers are characterized by the effective dielectric permittivity and conductivity for grain cores, grain boundaries and/or inter-grains. These effective parameters are temperature and/or frequency dependent.
The superparaelectric-like state with a giant dielectric response can appear in the paraelectric shells and inter-grain space due to the step-like thermal activation of localized polarons in the spatial regions, being in agreement with experimentally observed frequency-dependent transition of the electro-transport mechanism [3]. Obtained results can be the key for the description of complex electrophysical properties inherent to the strongly inhomogeneous media with electrically coupled insulating ferroelectric nanoregions and semiconducting superparaelectric-like regions.
The work of A.N.M. and E.A.E. are funded by the National Research Foundation of Ukraine (projects “Manyfold-degenerated metastable states of spontaneous polarization in nanoferroics: theory, experiment and perspectives for digital nanoelectronics”, grant N 2023.03/0132 and “Silicon-compatible ferroelectric nanocomposites for electronics and sensors”, grant N 2023.03/0127)
[1] K.W. Wagner, Arch Elektrotech 2, 371 (1914); https://doi.org/10.1007/BF01657322
[2] L. Liu, S. Ren, J. Liu, F. Han, J. Zhang, B. Peng, D. Wang, A. A. Bokov, and Z.-G. Ye, Phys. Rev. B 99, 094110 (2019), https://doi.org/10.1103/PhysRevB.99.094110
[3]. O. S. Pylypchuk, S.E. Ivanchenko, M.Y. Yelisieiev, A. S. Nikolenko, V.I. Styopkin, B. Pokhylko, V. Kushnir, D.O. Stetsenko, O. Bereznykov, O.V. Leschenko, E.A. Eliseev, V.N. Poroshin, N.V. Morozovsky, V.V. Vainberg, and A.N. Morozovska. https://doi.org/10.48550/arXiv.2407.01108 (http://arxiv.org/abs/2407.01108)

Speaker: Eugene Eliseev (Frantsevich Institute for Problems in Materials Science, National Academy of Sciences of Ukraine)

17:15 Model of effective permittivity for dense ferroelectric nanocomposites

Existing theoretical models of ferroelectric nanocomposites use the effective medium approximation to describe their dielectric and conductive properties. The most common effective medium models (Landau linear mixture approximation, Maxwell-Garnett model, Bruggeman model, etc.) may be invalid for dense nanocomposites when the volume fraction of ferroelectric inclusions exceeds 20-30%. We have proposed several modifications, such as averaging over particle size, finite conductance of the screening shell, and the dipole-dipole cross-interaction effects between the electric polarization (i.e., their electric dipoles) of different ferroelectric nanoparticles separated by shells and a matrix.
The Lichtenecker-Rotter model, which is free from the volume fraction limitations, was used to estimate the effective dielectric constant $\epsilon_{eff}$ of the nanocomposite without taking into account the effects of cross-interaction. However, the presence of small particles (size 30 nm or less) should be taken into account, as dipole-dipole cross-interactions can lead to the formation of polar clusters, where the ferroelectric dipoles of single-domain nanoparticles are strongly correlated, and the correlations determine the effective dielectric response of the composite.
The presence for larger submicron particles (size 300 nm or more), which usually split into ferroelectric domains, the cross-interaction effects can lead to correlated motion of ferroelectric domain walls in neighboring nanoparticles, which, in turn, make a significant contribution to the temperature and frequency behavior of the dielectric response of the composite.
The dependence on $\epsilon_P(T, \theta, \omega)$ of the frequency $\omega$ and the temperature of the local transition $\theta$ of nanoparticles and their polar clusters in a ferroelectric polymer nanocomposite was analyzed taking into account the dipole-dipole cross-interactions. As a result, the equation for $\theta$. was obtained. This equation was successfully applied to calculate the dielectric constant of dense PVDF nanocomposites with 20-30 vol.% of barium titanate nanoparticles. The obtained results can be used for the prediction and development of the flexible and cheap nanocomposite with superior polar and dielectric properties for usage in non-volatile memory cells, energy-saving elements, modulators and sensors.

The work of P.O.S. and M.A.N. is funded by the National Research Foundation of Ukraine (project “Manyfold-degenerated metastable states of spontaneous polarization in nanoferroics: theory, experiment and perspectives for digital nanoelectronics”, grant N 2023.03/0132)

Speaker: Oleksii Bereznykov

17:20 DNA condensation induced by Li$^+$ counterions

DNA is a highly charged molecule that is neutralized by positively charged metal or molecular ions (counterions). The neutralization of DNA by these counterions induces various effects, including the formation of DNA-DNA contacts that lead to further condensation of the macromolecule. The effect of DNA condensation has been widely observed for highly charged counterions (≥3+). For divalent counterions, DNA condensation is sometimes observed, whereas with monovalent ions, it is generally considered impossible due to insufficient neutralization of the double helix's charge required to form stable DNA-DNA contacts. However, the idea that DNA cannot condense with monovalent ions overlooks the interplay between water molecules in the DNA hydration shell and those in the hydration shell of counterions, which can play an essential role in the interaction of DNA duplexes. Li$^+$ is highly hydrated and it is localized within a stable tetrahedron formed by four oxygen atoms of water molecules. Considering the structural complementarity of the DNA phosphate groups to the hydration shell of Li$^+$ ions [1], the formation of Li-mediated DNA-DNA contacts may occur. To elucidate the possibility of forming stable Li$^+$ crosslinks between different DNA double helices, the molecular mechanisms of their formation are studied in the present work. Atomistic molecular dynamics simulations of five DNA fragments in a simulation box with LiCl concentration 0.1 M and 1.0 M of salt were carried out. As a result of our study, the possible configurations of crosslinks between phosphate groups of different DNA fragments were determined. To validate the obtained results, the vibrational spectra of characteristic complexes were calculated using quantum-chemical methods and compared with existing experimental data. This work demonstrates that DNA-DNA contacts mediated by Li$^+$ can form in aqueous solutions with a high concentration of DNA and LiCl salt, supporting the idea of DNA condensation by Li$^+$ counterions.

[1] Lyubartsev, A. P.; Laaksonen, A. Molecular Dynamics Simulations of DNA in Solution with Different Counter-Ions. J. Biomol. Struct. Dyn. 1998, 16 (3), 579–592. https://doi.org/10.1080/07391102.1998.10508271.

Speaker: Dmytro Piatnytskyi (Bogolyubov Institute for Theoretical Physics)

17:25 The electric field quantum control of spin-waves dynamics in easy-axis antiferromagnets

O. O. Boliasova$^{1,2}$ and V. N. Krivoruchko$^3$
$^1$State Research Institution «Kyiv Academic University»
36 Academician Vernadsky Boulevard, 03142, Kyiv, Ukraine,
$^2$G. V. Kurdyumov Institute for Metal Physics of the N.A.S. of Ukraine
36 Academician Vernadsky Boulevard, 03142, Kyiv, Ukraine, and
$^3$Donetsk Institute for Physics and Engineering named after O.O. Galkin of the NAS of Ukraine,
46 Nauki Avenue, 03028, Kyiv, Ukraine

Magnetic materials are widely used in current computers and have the potential to expand their applicability [1]. The most important step forpractical applications is understanding how to manipulate spin dynamics in magnetic materials efficiently. One method that has been actively discussed is usingan electric field. It is well known that spin waves with different chirality exist in antiferromagnets, however, in the absence of external influence these spin waves are degenerated. An electric, E, field can split them and manipulate each polarization differently. This phenomenon is an example of a topological effect known asthe Aharonov-Casher effect [2,3]. In the linear order approximation, this effect can be accounted for by adding a term to the system’s free energy expression like the Dzyaloshinskii-Moriya interaction.
We present the results on the E-field effect on chirality-dependent spin-waves dynamics in a two-sublattice easy-axis antiferromagnet [4,5]. The research was conducted using a phenomenological approach based on the Landau-Lifshitz-Gilbert equations. It was shown that the electric field can split spin waves of different chirality, and the magnitude of the splitting is proportional to the magnitude of the electric field. This splitting can be further enhanced by applying a magnetic field. More details are provided on the E-field effect on the propagation of spin waves and their damping length. The electric field affects the propagation of the right-handed and left-handed spin waves differently, while a small magnetic field doesn`t influence the damping length. These findings could be useful for field-effect transistors or interferrometric devices [6] based on spin waves. Since the application of the electric field is easier than that of a large magnetic field, the Aharonov-Casher effect has great potential for practical applications.
The authors acknowledge the financial support by the STCU, project “Magnetism in Ukraine Initiative”, project Agreement No. 9918.

Speaker: Olha Boliasova (State Research Institution «Kyiv Academic University»)

17:30 Supercritical propagation of nonlinear magnetization wave through an antiferromagnetic magnonic crystal

Analytical model of a nonlinear magnetization wave (MW) propagating through one-dimensional antifer-romagnetic magnonic crystal comprised of two sorts of antiferromagnets (AFM) is proposed for supercritical mode when the MW velocity exceeds the critical velocity of MW in both antiferromagnets AFMs or at least in one of them. Both AFMs that comprise the magnonic crystal are assumed to be two-sublattice uniaxial ones. The Landau-Lifshitz equations have been used in the sigma model with account for the exchange bias between magnetic sublat-tices of both AFMs, the magnetic anisotropy, the magnetic dipole-dipole interaction and the Dzyaloshynskii-Moriya interaction. The boundary conditions for the Néel vector (with the exchange bias between magnetic sublattices of both AFMs taken into account) are applied on the interface between two AFMs. The discrete sets of frequencies and velocities for the considered MW are obtained. Analysis of the results shows that the nonlinear MW is reflection-less, phase-coherent and possesses a number of parameters that can be considered as degrees of freedom for encod-ing information. These findings open up new possibilities of digital data processing utilizing nonlinear MW propa-gating through antiferromagnetic magnonic crystal in supercritical mode.

Speaker: Ihor Syzon (National Technical University of Ukraine «Igor Sikorsky Kyiv Polytechnic Institute»)

17:35 Evaluating Benchmarks for the Effectiveness of Infrared Camouflage Coatings

Contemporary research in defense technology focuses extensively on concealing various objects from infrared (IR) reconnaissance. Numerous camouflage coatings are available in the market, designed to mask IR radiation emitted by targets. Manufacturers often claim that these coatings significantly reduce the mean apparent temperature difference (ΔT) between the object and its background. However, a critical scientific question remains: how does the reduction in ΔT correlate with the actual decrease in maximum detection range (MDR) achieved by thermal imaging systems?

A wide range of cooled and uncooled portable thermal imagers exists for the 3-5 μm and 8-12 μm spectral ranges. Their detection capabilities are constrained by both spatial resolution and thermal sensitivity, characterized by the noise equivalent temperature difference (NETD). To estimate the MDR reduction due to target temperature contrast masking, it is valuable to evaluate the MDR for several commercially available thermal imagers at distances where their sensitivity for chosen object size is not restricted by spatial resolution. According to NATO Standard STANAG 4347, the MDR for a target can be determined by graphically solving an equation. The left-hand side of this equation represents the simple exponential decay of ΔT with distance, while the right-hand side denotes the minimum resolvable temperature difference (MRTD) of the thermal imager, which is also dependent on distance and target dimensions. The MRTD for a high-resolution thermal imager in the 3-5 μm range was obtained from literature [1].

Our modeling aimed to assess how a 50% reduction in target ΔT affects the MDR and to evaluate the significance of this change relative to potential variations due to adverse weather conditions. We modeled targets with ΔT = 4 K (uncamouflaged) and ΔT = 2 K (camouflaged), using atmospheric absorption coefficients of k = 0.2 1/km (good transmission conditions) and k = 1 1/km (limited transmission conditions). The dimensions of the test target were set at 1x1 m2.

The modeling results for the 3-5 μm range are presented in the Figure 1. The MDR is determined at the intersection point of the ΔT and MRTD curves. Our findings indicate that a 50% decrease in ΔT has only a slight impact on MDR reduction under any weather conditions. Consequently, effective IR camouflage coatings should provide a substantially greater reduction in the observed temperature difference between the target and background. Furthermore, our modeling revealed that the MDR for a target with a fixed ΔT can vary by several times depending on weather conditions. Similar modeling was also conducted for the 8-12 μm range.

This study was supported by NRFU project #2023.04/0026.

1. Barela, J., Firmanty, K., & Kastek, M. (2021). Measurement and analysis of the parameters of modern long-range thermal imaging cameras. Sensors, 21(17), 5700. https://doi.org/10.3390/s21175700.

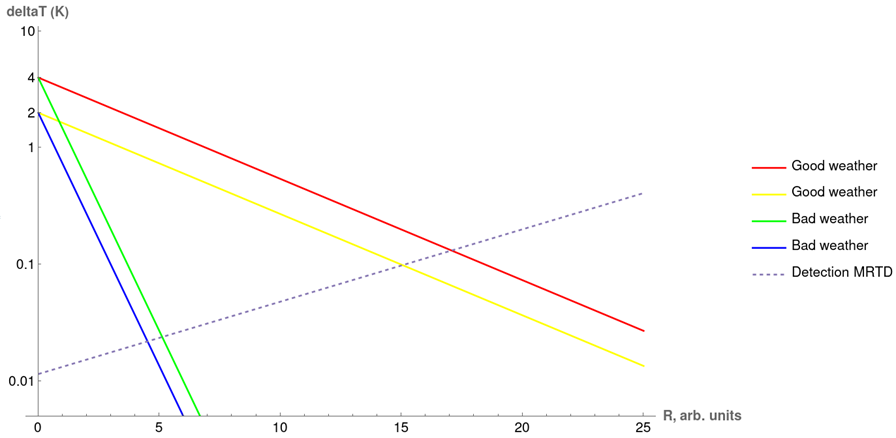
Fig.1. The modeling results for the 3-5 μm range MDR for variable weather conditions, for camouflaged and uncamouflaged target.

Speaker: Ye.O. Melezhyk (V. Lashkaryov Institute of Semiconductor Physics, NASU)

BITP-2024-Melezhyk_Fig-1.png

17:40 Invisible states Potts model

The Potts model with invisible states was introduced to explain discrepancies between theoretical predictions and experimental observations of phase transitions in some systems where Zq symmetry is spontaneously broken [1]. It differs from the ordinary q-state Potts model in that each spin, besides the usual q visible states, can be also in any of r so-called invisible states. Spins in an invisible state do not interact with their neighbours but they do contribute to the entropy of the system. As a consequence, an increase in r may cause a phase transition to change from second to first order. Potts models with invisible states describe a number of systems of interest in physics and beyond and have been treated by various tools of statistical and mathematical physics. We aim to give a review of this fundamental topic based on our results [2-4]. Mainly, our goal was to investigate the energy-entropy interplay influence on the phase transition in the Potts model with invisible states in 1D case [2] as well as on different graph topologies [3].
We acknowledge support from the National Research Foundation of Ukraine, Project 2023.03/0099 "Criticality of complex systems: fundamental aspects and applications".

[1] S. Tanaka, R. Tamura, N. Kawashima. J. Phys. Conf. Ser., 297 (2011) 012022.
[2]. Petro Sarkanych, Yurij Holovatch, Ralph Kenna. Journ. Phys. A vol. 51 (2018) 505001; Phys. Lett. A vol. 381, (2017) 3589-3593
[3] M. Krasnytska, P. Sarkanych, B. Berche, Yu. Holovatch, R. Kenna. J. Phys. A: Math. Theor., 49(25) (2016) 255001;
P. Sarkanych, M. Krasnytska. Cond. Matt. Phys., 26 (1) (2023) 13507.
[4] M. Krasnytska, P. Sarkanych, B. Berche, Yu. Holovatch, R. Kenna. Eur. Phys. J. Spec. Top. 232, 1681–1691 (2023).

Speaker: Mariana Krasnytska (Institute for Condensed Matter Physics, National Acad. Sci. of Ukraine, Lviv, 79011, Ukraine)

17:45 Influence of the pH of aqueous sodium chloride solutions with dissolved carbon dioxide on the temperature interval of human vital activity

Temporal changes in the temperature and concentration dependences of the pH value in aqueous sodium chloride solutions contacting with atmospheric carbon dioxide have been studied experimentally. The measurements are carried out in a temperature interval of (294–323) K for ion concentrations corresponding to (180–1600) water molecules per sodium or chlorine ion.
The pH value for dilute aqueous solutions of sodium chloride is a sum of two components: reducible and irreducible. The reducible component depends linearly on the temperature and, therefore, cannot be responsible for the specific details of the human and mammalian life activities. Therefore, the main parameters of the latter have to be characterized by the irreducible pH component, which is an order of magnitude smaller than the reducible component. The proportionality between the irreducible pH component value and the sodium chloride concentration may testify that minor pH changes are associated with corresponding changes in the salt composition of blood plasma that affect the state of human organism.
The pH relaxation time in aqueous NaCl solutions with dissolved atmospheric carbon dioxide and its dependence on the temperature and the ion concentration are calculated. The analysis of the obtained temperature dependences of the pH relaxation time testifies that they are similar for various concentrations of NaCl ions in water. The principle of natural selection of the optimal states of aqueous salt solutions characterized by the temperature and the irreducible component of pH has been formulated for the first time: optimal are those states in which the pH relaxation time in aqueous salt solutions is minimum.
The minimum points in the curves of the irreducible pH component for aqueous sodium chloride solutions are directly related to the temperatures that can be interpreted as the lower (approx. 30°C) and upper (approx. 42°C) limits of the temperature interval of the human and mammalian life activities. At the same time, the minimum in a vicinity of the temperature of 37°C can be interpreted as the optimal temperature for the vital activity of humans and mammals.
Since the reducible and irreducible pH components behave themselves differently, of particular importance becomes the issue concerning the conformational modifications of human serum albumin and other proteins, which depend on the pH value. The addition of proteins will change the reducible pH component, and the conformational modification of albumin will be primarily induced by the electric fields of hydrogen cations, which will directly affect the irreducible pH component.

[1] L.A. Bulavin, N.P. Malomuzh, O.V. Khorolskyi. Reducible and irreducible components of the pH value in dilute aqueous solutions of sodium chloride. Ukrainian Journal of Physics, 2023, 68(3), 177–183. https://doi.org/10.15407/ujpe68.3.177

Speaker: Oleksii Khorolskyi (Poltava V.G. Korolenko National Pedagogical University)

17:50 Features of the temperature dependences of the thermal conductivity of composites and the Meyer-Neldel rule

An analysis of the temperature dependences of thermal conductivity κ(Т) of composite materials - graphene-multilayer graphene, semiconductor composites Bi0.5Sb1.5Te3 and In0.53Ga0.47As, was carried out as well as a comparison of their temperature dependences of κ(Т) with the thermal conductivity of similar materials, which are formed by superlattices, nanowires and hybrid nanostructures. The temperature dependence of the thermal conductivity κ(Т) of these materials can be presented as the sum of two contributions – quasi-particle κp and coherence contributions κc:
$κ = κp + κc$, (1)
which corresponds to two main mechanisms of heat transfer [1]. In the case of orientationally ordered crystals, thermal conductivity, as a rule, can be represented as:
$κ = AT-1 + κ0$, (2)
where the first term is determined by the three-phonon scattering processes of quasiparticles (phonons), and the second term is related to the wave properties of phonons and their ability to tunnel between phonon bands corresponding to the acoustic and optical phonon branches in the real dispersion law [1].
In the case where long-range order is present, the value of the coherent contribution κc is usually small compared to the quasi-particle contribution κp, but it becomes significant when no translation order - then it takes place the glass-like behavior of thermal conductivity – and it can be presented through an exponential dependence of the Arrhenius type:
$κc = κ0∙exp(-E/T)$ (3)
with two characteristic parameters: pre-exponential factor κ0 and energy E. It was shown that the temperature dependences of thermal conductivity with glassy behavior are quite well described by expression (3). Also, it is established that the pre-exponential factor κ0 depends linearly on the energy E. Such a relationship between these values was previously discovered in the electrical conductivity of semiconductors (Meyer-Neldel rule) [2, 3].

References:
[1] A.I. Krivchikov, Y.V. Horbatenko, O.A. Korolyuk, O.O. Romantsova, O.O. Kryvchikov, D. Szewczyk & A. Jezowski. Exponential approximation of the coherence contribution to the thermal conductivity of complex clathrate-type crystals. Materialia, 32, 101944 (2023).
[2] A.I. Krivchikov & O.A. Korolyuk. Empirical universal approach to describing the thermal conductivity of amorphous polymers: Effects of pressure, radiation and the Meyer–Neldel rule. Low Temperature Physics, 50(4), 328-341 (2024).
[3] W.V. Meyer and H. Neldel. Relation between the energy constant and the quantity constant in the conductivity–temperature formula of oxide semiconductors, Z. tech. Phys., 18(12): 588–593 (1937).

Speaker: Dr Yuliia Horbatenko (B.Verkin Institute for Low Temperature Physics and Engineering of the National Academy of Sciences of Ukraine)

17:55 Influence of the unit cell size of periodic electromagnetic metamaterials on their optical properties

To date, the most of metamaterials used in diverse applications (from nanooptics and plasmonics to mobile communication and biophysics) are periodic structures consisting of spatially arranged inclusions. In the theory of metamaterials, they are treated as homogeneous media, if their unit cell size $d$ (the lattice constant) is much smaller than the wavelength $\lambda$ of the incident electromagnetic wave the metamaterials operate with, $d \ll \lambda$. A number of homogenization theories have been proposed to calculate metamaterial's effective parameters, such as the effective permittivity $\varepsilon_{\textrm{eff}}$, permeability $\mu_{\textrm{eff}}$, and index of refraction $n_{\textrm{eff}}$, based on the geometry and material parameters of the metamaterial's inclusions. In practice, however, condition $d \ll \lambda$, or, equivalently, $d / \lambda \ll 1$, is not always met.

In the present work, the properties of metamaterials are analyzed in a wider range of their relative unit cell size $d / \lambda$ values for several types of the metamaterials' inclusions of practical interest. The optical reflectance $R$ and transmittance $T$ of the metamaterials are numerically calculated based on the Lorentz volumetric averaging of the local electric and magnetic fields inside the unit cells, rather than using recent metamaterials homogenization theories proposed in the last two decades.

It is shown that behavior of the optical properties of metamaterials declines more and more from what is expected based on the homogenization concept, as the relative unit cell size increases from small values $d / \lambda \ll 1$ (the quasistatic regime) to the unity (the intermediate operating regime). In the latter regime, a crucial role in the optical properties formation play the diffraction and interference effects in the metamaterials, and the properties exhibit an oscillating behavior which cannot be predicted within the homogenization concept.

Publications:

V. V. Gozhenko, A. K. Amert, and K. W. Whites, Homogenization of periodic metamaterials by field averaging over unit cell boundaries: use and limitations, New J. Phys. 15, 043030 (2013) https://doi.org/10.1088/1367-2630/15/4/043030

Victor V. Gozhenko, Size Effects in Periodic Metamaterials, arXiv:2301.03518 [physics.optics] (2023) https://doi.org/10.48550/arXiv.2301.03518

Speaker: Victor Gozhenko (Institute of Physics, National Academy of Sciences of Ukraine)

Poster.pdf

17:55 Low temperature behavior of the heat capacity of MWCNTs with Ø9.4 nm: component of flexural dispersion for phonons

M.S. Barabashko1, M.I. Bagatskii1, V.V. Sumarokov1, A.I. Krivchikov1,
A. Jeżowski2, D. Szewczyk2,3, Y. Horbatenko1

1B.Verkin Institute for Low Temperature Physics and Engineering of NAS of Ukraine,
47 Nauky Ave., Kharkiv, 61103, Ukraine
2 W. Trzebiatowski Institute for Low Temperatures and Structure Research, Polish Academy of Sciences,
P.O. Box 1410, 50-950 Wroclaw, Poland
3Low Temperature Laboratory, Condensed Matter Physics Department, Universidad Autónoma de Madrid, Madrid, Spain

e-mail: msbarabashko@gmail.com

Low-temperature specific heat C(T) of multi-walled carbon nanotubes (MWCNTs) was studied. Two sets of modified, milled and milled-oxidized MWCNTs with an average outer diameter of 9.4 nm were used to measure specific heat in the temperature range of 1.8 to 275 K. The experimental results were compared with literature data for different carbon systems: bundles of single-walled carbon nanotubes (SWCNTs), graphite and other MWCNTs.
The initial MWCNTs were obtained by the CVD method. The length of MWCNTs and parameters of defects (number and types) in MWCNTs were changed: 1) grinding of the initial nanotubes in a ball mill; 2) the initial nanotubes were first oxidized and then milled. The figure shows low-temperature experimental heat capacity curves of ground (Sm), ground-oxidized (Sm-o) MWCNTs with outer diameters of Ø9.4 nm, as well as, for comparison, original nanotubes (Si), bundles of SWNCTs (Ø1.1 nm) and graphite. The analysis of the low-temperature behavior of the heat capacity of carbon materials below 3 K was carried out under the assumption that C(T) is determined primarily by phonons with sufficiently long wavelengths (deformation waves). The specific heat C(T), described by the equation C(T) = AT + BT3+ D*T5. The coefficients A, B and D were calculated and analyzed. The decrease in the length of nanotubes and the appearance of defects as a result of both grinding and oxidation with subsequent grinding lead to an increase in heat capacity in the low-temperature region. The obtained negative D parameter indicated flexural dispersion for phonons. It was found that the magnitudes of the Debye (B) and flexural dispersive components (D) depend on the structural parameters of nanotubes: such as the diameter of individual nanotubes, the average diameter of the bundle and the size of agglomerates.

Acknowledgments:
This work has been supported by the National Research Foundation of Ukraine

Speaker: Yuliia Horbatenko (B.Verkin Institute for Low Temperature Physics and Engineering of the National Academy of Sciences of Ukraine)

Wednesday, 25 September

10:00 → 13:30 Morning Session 2

10:00 On a crossover between two mechanisms of sound propagation in liquids

Hydrodynamic theory forms the basis for our understanding of the macroscopic propagation
of sound in liquids, while viscoelasticity points out solid-like elastic features at large frequencies. However, there is no understanding how the viscoelasticity manifests in the mechanism of propagation of mesoscopic and short-wavelength acoustic excitations in liquids.
We report solutions of the generalized Langevin equation for density-density time correlation functions of a liquid system in terms of dynamic eigenmodes within viscoelastic and thermo-viscoelastic dynamic models. A comparison with molecular dynamics somputer simulations for supercritical Ar is performed. It is shown by analysis of extended dynamic eigenmodes in liquids how the crossover from hydrodynamic mechanism of sound propagation to elastic one takes place. Our analysis of wavenumber-dependent eigenvector components of the sound modes makes evidence that the viscoelasticity of sound excitations is originated by gradual replacement of contribution from hydrodynamic density fluctuations by non-hydrodynamic stress fluctuations. A consequence of the sound viscoelasticity for emergence of structural relaxation is shown.

Speaker: Taras Bryk

10:40 Quantum topological effects in magnetization dynamics: the Berry phase, the Aharonov–Casher effect and electric field control of spin waves dynamics

Condensed matter physics is revolutionizing by introducing topology-based concepts that characterize a system's physical states and properties. An example of topological effects in magnetization dynamics is the additional quantum mechanical phase, the so-called Berry phase [1], and the Aharonov–Casher (AC) effect [2], acquired by the quantum orbital motion of chargeless bosonic quasiparticles with magnetic dipole moment – e.g., spin waves (SWs) with magnetic moment µm = ±gµB – in mesoscopic rings in an external electric (E) field. It manifests itself in a shift of the dispersion and the group velocity direction of SW by the E field. In the linear approximation concerning the electric field, the magnonic AC effect can be considered by adding the Dzyaloshinskii-Moriya-like interaction between neighboring spins. This topological quantum phenomenon has been directly detected experimentally for SWs propagating in the classical magnetic insulator Y3Fe5O12 [3,4]. The magnitude of the AC phase was two orders larger than previously estimated theoretically for centrosymmetric ferromagnet insulators. This finding allows for tuning the properties of SWs, an essential ingredient for magnonic devices, by the E-field. Through analytical calculations and micromagnetic simulations, we demonstrated that in ferromagnetic, antiferromagnetic, and ferrimagnetic nanoscale films, it is possible to control the SWs characteristics using an external E-field [5-9]. From the fundamental point of view, the discussed quantum phenomena open a new avenue for quantifying topological effects in magnetization dynamics. The E-field control of SW dynamics in magnetic film can also be helpful for the development and designing of new magnonic nanodevices and could be utilized for quantum technologies.
V.N.K. acknowledges the financial support by the STCU, project “Magnetism in Ukraine Initiative”, project Agreement No. 9918.

[1] M. V. Berry. Quantum phase factors accompanying adiabatic changes. Proc. R. Soc. London, Ser. A 392, 45 (1984).
[2] Y. Aharonov, A. Casher. Topological quantum effects for neutral particles. Phys. Rev. Lett. 53, 319 (1984).
[3] X. Zhang, T. Liu, M. E. Flatté, H. X. Tang. Electric field coupling to spin waves in a centrosymmetric ferrite. Phys. Rev. Lett. 113, 037202 (2014).
[4] R. O. Serha, V. I. Vasyuchka, A. A. Serga, B. Hillebrands. Towards an experimental proof of the magnonic Aharonov-Casher effect. Phys. Rev. B 108, L220404 (2023).
[5] V. N. Krivoruchko, A.S. Savchenko, V. V. Kruglyak. Electric-field control of spin-wave power flow and caustics in thin magnetic films. Phys. Rev. B 98, 024427 (2018).
[6] V. N. Krivoruchko, A.S. Savchenko. Electric-field control of nonreciprocity of spin wave excitation in ferromagnetic nanostripes. J. Magn. Magn. Mater. 474, 9 (2019).
[7] V. N. Krivoruchko. Aharonov–Casher effect and electric field control of magnetization dynamics. Low Temp. Phys. 46, 820 (2020).
[8] O. Boliasova, V. Krivoruchko. Electric-Field Control of Magnetization Dynamics in Antiferromagnets. 2023 IEEE Nanotechnology Materials and Devices Conference (NMDC), Paestum (Salerno), Italy; DOI:10.1109/NMDC57951.2023.10343910
[9] V. N. Krivoruchko, A.S. Savchenko. Controlled refraction and focusing of spin waves determined by the Aharonov-Casher effect. Phys. Rev. B 109, 184437 (2024).

Speaker: Prof. Volodymyr Kryvoruchko (Donetsk Physics & Technology Institute named after O. O. Galkin, NAS of Ukraine, 46, Nauki Avenue, 03028 Kyiv)

11:20 Critical Behavior of Structurally Disordered Systems Magnets with Long-Range Interaction

Our research aims to examine critical behavior of a magnetic system under the influence of two competing factors: long-range interaction and weak structural disorder (e.g., weak quenched dilution). We analyze ferromagnetic ordering in a structurally-disordered magnet within an $n$-vector model in $d$-dimensional space, where the long-range interaction decays with distance $x$ as $J(x) \sim x^{-d -\sigma}$, where with $\sigma$ as is the control parameter. Field-theoretical renormalization group methods (RG) are used to identify the system’s universality classes, and the universal characteristics of critical behavior depending on the global parameters $d, n, \sigma$. We demonstrate that there exists a parameter region $(d, n, \sigma)$, where the interplay of long-range interaction and structural disorder leads to emergence of a new structural-disorder-induced long-range universality class. Using fixed spatial dimension approach we extract values of correlation length critical exponent $\nu$ characterizing this class from perturbative RG functions at $d = 3$ applying asymptotic series resummation methods.

This work was supported by the National Research Foundation of Ukraine, Project 246/0099 "Criticality of complex systems: fundamental aspects and applications" .

Speaker: Dr Dmytro Shapoval (Institute for Condensed Matter Physics of the National Academy of Sciences of Ukraine; L4 Collaboration & Doctoral College for the Statistical Physics of Complex Systems, Leipzig-Lorraine-Lviv-Coventry, Europe)

11:40 Thermodynamics of the kagome Heisenberg antiferromagnets

Kagome-lattice Heisenberg antiferromagnet is a paradigmatic model in the field of frustrated magnetism that allows us to study the interplay of geometrical frustration and quantum as well as thermal fluctuations in two and three dimensions. Distinctive spectrum of this model manifest itself in the thermodynamic properties throughout the peculiar low-temperature behavior of the specific heat.

We use 16 terms of a high-temperature series expansion complemented by the entropy-method interpolation to examine the specific heat and the uniform susceptibility of the Heisenberg model on the three-dimensional kagome (hyperkagome) lattice. We obtain thermodynamic quantities for several scenarios determined by the behavior of the specific heat as the temperature tends to zero. All scenarios give rise to a low-temperature peak in $c(T)$ well below the main high-temperature peak. The functional form of the uniform susceptibility $\chi(T)$ below about $T=0.5$ depends strongly on the chosen scenario. An estimate for the ground-state energy $e_0$ depends on the adopted specific scenario but is expected to lie between $−0.441$ and $−0.435$. In addition to the entropy-method interpolation, we use the finite-temperature Lanczos method to calculate $c(T)$ and $\chi(T)$ for finite lattices of $N=24$ and $36$ sites.

This project is funded by the National Research Foundation of Ukraine (2023.03/0063, Frustrated quantum magnets under various external conditions).

Speaker: Taras Hutak (Institute for Condensed Matter Physics of the National Academy of Sciences of Ukraine)

12:00 Coffee break

12:30 Squeezing and amplification in open quantum systems with color centers using the multilevel Janes-Cummings model

The ability to couple cavity-confined microwave modes to diamond slabs or films containing large numbers of color centers opens up potential new methods for noise reduction, processing, and even generating quantum states of microwaves. The unique feature of various diamond color centers is that they can be prepared in their ground states by illuminating them with light in the optical band. The color centers then become a very low noise (effectively very low temperature) system for processing and manipulating microwaves.
Ensembles of few-level emitters are able to generate nonlinearities for electromagnetic fields. Often, this is done by arranging the level structure and driving to simultaneously induce the electromagnetically induced transparency to eliminate most of the absorption that can accompany nonlinearities due to the decay of the emitter energy levels. For color centers, the lowest lying spin levels, e.g., three levels for nitrogen-vacancy (NV) centers, have very long lifetimes, so this is not a significant issue. Ensembles of emitters will also generate nonlinearities for single modes, but the produced nonlinearities are limited to the maximal ones that can be generated by single emitters. Essentially, for the purpose of generating nonlinearities, having an ensemble effectively increases the coupling rate: if the coupling of each emitter is $g_0$, then an ensemble with $N$ emitters acts as a single emitter with a coupling rate $g =\sqrt{N}g_0$, which is valid for the off-resonant generation of nonlinearities.
An ensemble of two-level emitters off-resonant with a single mode generates a series of nonlinearities with effective Hamiltonians given by powers of the mode energy operator $a^\dagger a$. The first term in this series generates a frequency shift for the cavity mode proportional to ${g^2}/{\Delta} $, where $\Delta$ is a detuning between the NV-centers and the cavity mode. Modulating the frequency of a mode induces parametric amplification.
In this study we investigate the optimal modes of operation of a $N$-level atomic system interacting with the cavity mode to obtain squeezed states and amplification of the electromagnetic cavity mode signal. This is performed in the framework of the Janes-Cummings model for the $N$-level atomic system within the rotating wave approximation. For this purpose, perturbation theory, namely the Magnus expansion for the evolution operator, up to and including second order of smallness, was used.
R.O. and A.S. acknowledge support by the National Research Foundation of Ukraine under the call "Excellent Science in Ukraine", project No. 235/0073.

Speaker: Roman Ovsiannikov (NSC «Kharkov Institute of Physics and Technology»)

12:50 Domains and domain boundaries structure of benzene adsorbed on graphene

In our report, we review the domain boundaries in the structure of benzene monolayer adsorbed on a graphene sheet. It is shown in [1] that the monolayer’s structure can be complicated even for benzene, the simplest representative of the cyclic hydrocarbons. It was found in [2] that there exist two different energy states of the adsorbed benzene molecule: 1) the symmetric (hollow) unstable state, where the benzene molecule is placed right over the graphene hexagon; 2) the non-symmetric (stacked) stable configuration, where the benzene molecule’s center is placed above one of graphene atoms. The low-symmetry structure is characterized by the presence of six domains, known as star domains. The representatives of these domains at the graphene hexagonal layer are star vectors that describe transitions from symmetric high energy state into the stable low symmetric position.

[1]. Lykah, V. A., & Syrkin, E. S. (2022). Domains of the adsorbed benzene monolayer on graphene. Low Temperature Physics, 48(4), 353-358.
https://doi.org/10.1063/10.0009743

[2]. Alzahrani, A. Z. (2011). Structural and electronic properties of graphene upon molecular adsorption: DFT comparative analysis. Graphene Simulation, 1, 21–38.
https://doi.org/10.5772/20356

Speaker: Yevhenii Trotskyi (B. Verkin Institute for Low Temperature Physics and Engineering of the National Academy of Sciences of Ukraine)

Screenshot 2024-08-19 182736.png

13:10 Modeling temperature dynamics in non-uniform biological tissues under cryogenic impact

Physical and mathematical modeling is widely used to simulate cryoapplication processes. Mathematical modeling of this process [1,2] allows us to predict the temperature field of the frozen region. This makes it possible to determine the cryo-application time sufficient to destroy target cells and minimize damage to healthy cells under various experimental conditions. Moreover, simulation also predicts the depth of the cryoapplication impact, which can be difficult to measure in some situations in the living tissues. Then, we use temperature-dependent thermodynamical parameters of biological tissues to compare simulation with thermal imaging.
The problem with moving phase boundary is known as the Stefan problem. There are several ways to numerically solve that problem. One of them is gradually changing thermodynamic parameters close to the phase change boundary. This approach is effectively describing the freezing dynamics of a biological tissues. The appearance of solutes in water leads to change the freezing temperature in a range of temperatures around (-10C..-0.1C) due to change of solute concentration. By combining the usual thermal capacity with latent heat, we can define an effective thermal capacity. That allows us to solve the heat equation in 2D cylindrical geometry, see Fig. 1.
Generally thermodynamic properties of the biological tissues are highly dependent on temperature, so we have a non-uniform heat equation $\frac{\partial T}{\partial t}=\frac{1}{\rho C_\text{p}}\nabla k\nabla T$ . To solve this equation numerically, we use the finite differences method on a rectangular mesh to calculate the thermal balance of each node. Then we compare our results with thermal imaging of cryoapplication impact on rat skin [3].

Fig. 1. (a) Principal scheme of the cryo-application problem for 2D cylindrical geometry with radial symmetry, where there is the cryo-applicator with a temperature of liquid Nitrogen pressed 1-2mm inside the soft tissues. (b) Dynamics of the maximum radius and depth of the ice spot for several isotherms. Typically consists of 4 phases, I-freezing, II-thawing thin layer of ice around the main ice spot, III-usual thawing, IV-finish thawing.
Acknowledgments: This research is sponsored by the National Research Foundation of Ukraine (Grant No. 2022.01/0094).
[1] M. Rossi and Y. Rabin, in: Proc. Int. Conf. "Modeling, Simulation & Visualization Methods" (MSV 2007), CSREA Press, 187-193.
[2] Y. Rabin and A. Shitzer, J. Biomech. Eng., 1997, 119, 146-152.
[3] G. Kovalev et al., Problems of Cryobiology and Cryomedicine, 2020 30, 359-368

Speaker: Dr Sergey Shevchenko (B. Verkin ILTPE of NASU)

Fig1_ivakhnenko.png

13:30 → 14:30 Lunch

14:30 → 17:00 Afternoon Session 2

14:30 Effect of the photon subsystem on the magnetic properties of quantum gases in equilibrium with radiation

We study the impact of the photon subsystem on the magnetic properties of a mixture of quantum gases in thermodynamic equilibrium with it. Having proposed a simple model of the system, we obtain general equations describing the thermodynamic equilibrium of quantum gases of two-level atoms with photons. The resulting equations are solved at a temperature higher than the degeneracy temperature of all three components. The analysis of the solutions shows the non-trivial dependence of magnetic properties on photon density and intensity of the external magnetic field. An increase in photon density due to external sources can lead to an increase in both magnetization and density of excited atoms. Such a conclusion is not a priori trivial since a photon in a vacuum does not have a magnetic moment.

The authors acknowledge support by the National Research Foundation of Ukraine under the call “Excellence Science in Ukraine”, project No. 235/0073.

Speaker: Prof. Юрій Слюсаренко (Інститут теоретичної фізики імені О.І. Ахієзера, Національний науковий центр "Харківський фізико-технічний інститут", НАН України; Харківський національний університет імені В.Н. Каразіна; Національний університет «Львівська політехніка»)

15:10 Resetting random walks in a bounded chain

The search of a target of unknown location is often random and ineffective, especially when the search domain is spacious and there is a lot of detrimental trajectories. To get rid of them, thereby improving the search, interruptions of the latter with starting it from scratch can be a good strategy. Called resetting, such a manner is in fact inherent to many search processes at very diverse levels of organization.
Initiated by the seminal work [1] devoted to diffusion with resetting along an infinite chain, the study of resetting effects in various model systems has quickly become a flourishing branch of the theory of stochastic processes. The vast majority of corresponding works, however, concerns spatially continuous models, whereas their discrete counterparts ‒ such as random walks in lattices or networks ‒ are not less important. For the latter, there were practically no exact results even in one dimension.
In the present talk, the recent results [2] on the resetting effects in one of the basic model ‒ classical random walks with Poissonian resetting in a one-dimensional lattice ‒ are expounded at length. The model is analyzed in its general version, for arbitrary initial and boundary conditions, which lead to a variety of optimization scenarios illustrated by non-standard behavior of the main observables (splitting probabilities, mean first passage times, coefficients of variation). A quantum analog of the model is briefly discussed.

1. M.R. Evans, S.N. Majumdar. Phys. Rev. Lett. 106, 160601 (2011).
2. L.N. Christophorov. Rep. Natl. Acad. Sci. Ukraine (Dopovidi) 8, 43 (2020); J. Phys. A: Math. Theor. 54, 015001 (2021); J. Phys. A: Math. Theor. 55, 155006 (2022); Ukr. J. Phys. (2024).

Speaker: Leonid Christophorov (Bogolyubov Institute for Theoretical Physics, NAS Ukraine)

15:30 Application of Langevin dynamics for optimization in machine learning tasks

A rapid growth of Machine Learning (ML) applications in different areas has been faced in recent years. Training of ML models is performed by finding such values of their parameters $x=\{x_1, x_2, ..., x_N\}$ that optimize (minimize) the objective (loss) function $U(x)$. Usually, the number of parameters $N$ is large and the training dataset is massive. Therefore, to reduce computational costs, the gradient $f=-dU(x)/dx$ of the objective function with respect to the model parameters is computed on relatively small subsets of the training data, called mini-batches. If these mini-batches are selected randomly from the training dataset, then the estimated values of the loss $\hat{U}(x)$ and its gradient $\hat{f}=-d\hat{U}(x)/dx$ are the stochastic approximations of their exact values. Therefore, it is natural to apply Langevin dynamics to treat this stochastic optimization problem. We consider the next discrete form of the Langevin equation:

$\frac{\Delta x_{n+1} - \Delta x_{n}}{\Delta t^{2}} = \hat{f}_{n} - \gamma \frac{\Delta x_{n+1} + \Delta x_{n}}{2 \Delta t},$ (1)

where $n$ is an iteration number, $\Delta x_{n+1} = x_{n+1} - x_{n}$, $\Delta t$ is a time step and $\gamma>0$ is a viscous friction coefficient.
Now, it is straightforward to obtain the next parameter updating formula:

$\Delta x_{n+1} = \rho \Delta x_{n} + \hat{f}_{n} \cdot \eta,$ (2)

where $\rho = (1-\gamma \Delta t /2)/(1+\gamma \Delta t /2)$ is conventionally called a momentum coefficient and $\eta = \Delta t^{2}(1+\rho)/2$ a learning rate constant.
Equation (2) was derived in our recent work where we have introduced Coolmomentum – a method for stochastic optimization by Langevin dynamics with simulated annealing [1]. To implement simulated annealing (or slow cooling, in physical terms), we apply a certain schedule for the gradual momentum coefficient decrease in the range

$0 \leq \rho < 1$ (3)

In this talk we demonstrate that application of Langevin dynamics (2) with simulated annealing (3) to multidimension optimization tasks gives promising results in artificial intelligence [1], quantum computing [2] and optical engineering [3].

Acknowledgement: OB, MB and IO have received funding through the EURIZON project, which is funded by the European Union under grant agreement No.871072. AS acknowledges support by the National Research Foundation of Ukraine, project No.2023.03/0073.

[1] O. Borysenko, M. Byshkin, Sci Rep 11, 10705 (2021). https://doi.org/10.1038/s41598-021-90144-3.
[2] Daisuke Tsukayama et al. Jpn. J. Appl. Phys. 62, 088003 (2023). https://dx.doi.org/10.35848/1347-4065/acea0a.
[3] Z. Zhang et al. Photonics 10, 102 (2023). https://doi.org/10.3390/photonics10020102.

Speaker: Oleksandr Borysenko (National Science Center "Kharkiv Institute of Physics and Technology'")

15:50 Coffee break

16:20 Four types of phase transitions in interacting boson system at high temperatures

Within the framework of the mean-field model, the thermodynamics of the relativistic bosonic system of interacting particles and antiparticles in the presence of a Bose-Einstein condensate is investigated. It is assumed that the total isospin (charge) density is conserved. It is shown that the particle-antiparticle boson system reveals four types of phase transitions into the condensate phase. Three types belong to the phase transition of the second order and one to the first order. We show that the grand canonical ensemble is not suitable for describing a bosonic system of particles and antiparticles in the presence of condensate, but an adequate study can be carried out within the framework of the canonical ensemble, where the chemical potential is a thermodynamic quantity that depends on the canonical free variables.

Speaker: Dmytro Anchyshkin (Bogolyubov Institute for Theoretical Physics of the National Academy of Sciences of Ukraine, FIAS)

16:40 Chemical freeze-out curve in heavy-ion collisions and the QCD critical point

The chemical freeze-out curve in heavy-ion collisions is investigated in the context of QCD critical point (CP) search at finite baryon densities. Taking the hadron resonance gas picture at face value, chemical freeze-out points at a given baryochemical potential provide a lower bound on the possible temperature of the QCD CP. We first verify that the freeze-out data in heavy-ion collisions are well described by a constant energy per particle curve, $E/N = \rm const$, under strangeness neutrality conditions ($\mu_S \neq 0$, $\mu_Q \neq 0$). We then evaluate the hypothetical freeze-out curve based on this criterion in the absence of strangeness neutrality ($\mu_S = 0$, $\mu_Q = 0$) and confront it with recent predictions on the CP location. We find that recent estimates based on Yang-Lee edge singularities from lattice QCD data on coarse lattices place the CP significantly below the freeze-out curve and are thus disfavored by the heavy-ion data. On the other hand, predictions based on functional methods and holography place the CP slightly above the freeze-out curve, indicating that the QCD CP may be located very close to the chemical freeze-out in A+A collisions at $\sqrt{s_{NN}} = 3.5\div5$ GeV.

The report is based on a recently published article: https://arxiv.org/abs/2408.06473

Speaker: Artemiy Lysenko (Bogolyubov Institute of Theoretical Physics)

Thursday, 26 September

10:00 → 13:30 Morning Session 3

10:00 Analytical Description of Size Effects, Strains and Ferro-ionic Coupling in Si-Compatible Nanosized Ferroelectrics

The analytical methods based on the Landau-Ginzburg-Devonshire (LGD) approach and variational principle allow the analytical description of size effects, strain and ferro-ionic coupling in low-dimensional ferroelectric materials, such as thin films and small nanoparticles. The validity of LGD approach is corroborated by experimental evidence of the size- and strain-induced transitions as well as the related phenomena in the low-dimensional ferroelectric materials. For the correct description of these effects in ferroelectric thin films and small nanoparticles the LGD approach should be combined with the classical electrostatics and elasticity theory, and variational principle. It is important to determine how the LGD expansion coefficients depend on various factors, such as temperature, size, elastic stresses and/or strains, and ionic-electronic charge density and distribution. For classical ferroelectric films with a pronounced temperature-dependent and strain-dependent soft mode, the first expansion coefficients have a linear dependence on the temperature and elastic strain.
The significant attention is devoted to the comparison with experimental results and finite element modelling, as well as on the theoretical predictions of the size-, strain- and ionic- control of polar and dielectric properties of nanosized ferroelectric materials.
As the first example, we consider ultra-thin layers and nanoflakes of van der Waals ferrielectric CuInP2S6 covered by an ionic surface charge and reveal the appearance of polar states with relatively high polarization and stored free charge, which can mimic “mid-gap” states related with a surface field-induced transfer of Cu and/or In ions in the van der Waals gap [1]. The changes of the ionic screening degree and mismatch strains can induce the transitions between paraelectric phase, antiferroelectric, ferrielectric, and ferroelectric-like states in CuInP2S6 nanoflakes. Due to the emergence of manyfold-degenerated metastable states of spontaneous polarization the ultra-thin layers of CuInP2S6 reveal features of the controllable negative capacitance effect [2], which make them attractive for advanced electronic devices, such as nano-capacitors and gate oxide nanomaterials with reduced heat dissipation.
As the second example, we use the LGD model to quantify the strain-charge-polarization coupling in nanosized HfxZr1-xO2. A key factor ruling the observed polar properties of nanosized HfxZr1-xO2 is the presence of the polar orthorhombic phase. This phase is metastabile compared to the bulk monoclinic phase, leading to problems with the ferroelectric phase stability in nanoscale. The electrophysical properties of the HfxZr1-xO2 thin films and nanoparticles are very sensitive to the elastic strain induced by the substrate, annealing conditions, deposition method, film thickness, content x and dopants. Depending on the interplay of these factors, the nanosized HfxZr1-xO2 exhibits dielectric, ferroelectric, or antiferroelectric behavior.
The used model [3] incorporates parametrized Landau expansion coefficients for the polar and antipolar orderings. Obtained results agrees with the recent existing experimental data for HfxZr1-xO2-y thin films and oxygen-deficient HfO2-y nanoparticles [4], namely the X-ray diffraction confirmed the formation of a ferroelectric orthorhombic phase in the HfO2-y nanoparticles under special favorable annealing conditions.
The analytical LGD approach correctly predicts the phase diagrams, ground and metastable states, alongside the domain structure morphology, associated polar and structural properties of HfxZr1-xO2-y thin films and nanoparticles with different shapes and sizes. The successful application of the analytical LGD approach can be useful for the prediction of the silicon-compatible ferroelectric nanomaterials based on HfxZr1-xO2-y.
The work is funded by the National Research Foundation of Ukraine (projects “Manyfold-degenerated metastable states of spontaneous polarization in nanoferroics: theory, experiment and perspectives for digital nanoelectronics”, grant N 2023.03/0132 and “Silicon-compatible ferroelectric nanocomposites for electronics and sensors”, grant N 2023.03/0127).
[1]. Anna N. Morozovska, Sergei V. Kalinin, Eugene A. Eliseev, Svitlana Kopyl, Yulian M. Vysochanskii, and Dean R. Evans. Ferri-ionic Coupling in CuInP2S6 Nanoflakes: Polarization States and Controllable Negative Capacitance (2024), https://doi.org/10.48550/arXiv.2405.14368
[2]. Anna N. Morozovska, Eugene A. Eliseev, Yulian M. Vysochanskii, Sergei V. Kalinin, and Maksym V. Strikha. Size Effect of Negative Capacitance State and Subthreshold Swing in Van der Waals Ferrielectric Field-Effect Transistors, https://doi.org/10.48550/arXiv.2406.13051
[3]. Anna N. Morozovska, Maksym V. Strikha, Kyle P. Kelley, Sergei V. Kalinin, and Eugene A. Eliseev. Effective Landau-type model of a HfxZr1-xO2-graphene nanostructure, Phys. Rev. Applied 20, 054007 (2023) https://doi.org/10.1103/PhysRevApplied.20.054007
[4]. Eugene A. Eliseev, Yuri O. Zagorodniy, Victor N. Pavlikov, Oksana V. Leshchenko, Hanna V. Shevilakova, Miroslav V. Karpec, Andrei D. Yaremkevych, Olena M. Fesenko, Sergei V. Kalinin, and Anna N. Morozovska. Phase diagrams and polarization reversal in nanosized HfxZr1-xO2-y, AIP Advances, 14, 055224 (2024), https://doi.org/10.1063/5.0209123

Speaker: Prof. Anna Morozovska (Institute of Physics, National Academy of Sciences of Ukraine)

10:20 Sagnac effect in solids

The observation of the Sagnac effect for massive material particles offers a significant enhancement in sensitivity when compared to optical interferometers with equal area and angular rotation velocity. For this reason, there have been suggestions to employ solid-state interferometers that rely on semiconductors and graphene. We investigate the Sagnac effect in Dirac materials governed by the relativistic-like quasiparticle dispersion law and show that the fringe shift is still determined by the mass of a free electron. This confirms that graphene is indeed a promising material for creating solid-state Sagnac interferometers. Considering monolayer graphene with its linear dispersion law and comparing it with light provides a deeper understanding of the Sagnac effect.

Speaker: Dr Sergei Sharapov (Bogolyubov Institute for Theoretical Physics of the National Academy of Sciences of Ukraine Kyiv Academic University)

10:40 Impurity-induced localized modes in parallel Josephson junction arrays

We consider inhomogeneous underdamped one-dimensional parallel Josephson junction arrays. Inhomogeneity is introduced either as a non-uniformly applied dc bias current or as variations in the junctions' critical currents. We investigate the frequency of the localized modes induced by the presence of such inhomogeneities, in particular the frequency's dependence on the parameters that characterise inhomogeneities.

Speaker: Ms Daryna Bukatova (Bogolyubov Institute for Theoretical Physics)

11:00 Recursive Method for Calculating T-Matrix of Electron Scattering on Arbitrary Many-Particle Clusters in Strongly Correlated Systems

The generalized recursive method for calculating the T-matrix of electron scattering on arbitrary many-particle clusters for determining the Green's function of the strongly correlated system is developed. This approach is extended to the studying electronic spectra in both direct (Wannier) and reciprocal (Bloch) representations with taking into account the influence of atomic and magnetic correlations arising in the system at a temperature of 0 K. The one-band Hubbard model, the correlated random field approximation, and the one-site coherent potential approximation for the effective Hamiltonian of system are also used in this approach. The spectral density in reciprocal space is calculated in the same way (the same scheme) as in direct space, using the appropriate expressions for the effective Green's function, which includes contributions from all crystal sublattices. Calculation of the small parameter of the cluster expansion of the Green's function in direct and reciprocal representations shows its smallness for different parameters of b.c.c alloys. This ensures the convergence of obtained recursive formulas for T-matrix of scattering on many-particle clusters and the applicability of pairwise approximation for T-matrix. It should be noted that to calculate the configuration-averaged Green's function it is necessary to use at least the pairwise approximation of T-matrix for describing the influence of the cluster environment of each atom on the redistribution of charge and spin densities on atoms, as well as atomic and magnetic correlations. In addition, the possibility of nanoclusters formation and their influence on the magnetic state was investigated in the b.c.c. alloy with strong electron correlations. The calculation of electronic spectra in the reciprocal (as in direct) representation showed the high sensitivity to the changes in the characteristics and composition of the b.c.c. alloy including the nanoclusters formation as well as to the change of resulting short-range atomic and magnetic orders. This method could be useful to analyze experimental data obtained, for example, in positron spectroscopy to study electronic structure, defects, chemical composition, and various correlations in systems.
Key words: Green's function for strongly correlated alloys, recursive expression for T-matrix, arbitrary many-particle clusters, short-range atomic and magnetic ordering.

Speaker: Dr Tatiana Shatnii (G. V. Kurdyumov Institute for Metal Physics, N.A.S. of Ukraine)

11:20 Stimulating exitable membrane of ORN with stochastic Markov process

Excitable membrane of olfactory receptor neuron (ORN) is populated with up to several millions of identical receptor proteins (R) able to bind / release odor (O) molecules. The affinity of R to O depends on the odor presented, and this is the initial mechanism which is recuired for the olfactory selectivity to exist.

Figure 1: Simplified R structure. Modified from [3].

The affinity of R to O depends on the odor presented, and this is the very first step the olfactory selectivity builds up. Recently, [1], it was shown for a so called membrane-less ORN model that its selectivity can be much better than that of its R. A more realistic ORN model should include an excitable membrane with its electric transients. This introduces time parameter into the ORN's response to stimulation. The latter renders inappropriate used in [1] reasoning in terms of binomial distribution, and necessitates consideration of temporal properties of O binding-releasing and the membrane charging-discharging-firing.

In this contribution, we develop an approach in which the number of R bound with O $n(t)$, is modeled as a Markov stochastic process. With each bound R,
as it is observed for insects [2], Fig. 1, we associate an open channel having conductance 0.015 nS, which injects a depolarizing current through the membrane.
The futher membrane evolution is governed by the leaky integrate-and-fire neuronal model, see Eq. (1).
$c_M\frac{dV(t)}{dt}=-g_l(V(t)-V_{rest}) - n(t)g_{R}(V(t)-V_{e})$,
where $V(t)$ --- is the membrane voltage; $V_{rest}$ --- is the resting voltage;
$c_M$ --- is the total capacity of ORN's membrane;
$g_l$ --- is the total leakage through it;
$V_{e}$ --- is the reversal potential for current through open $R$;
$n(t)$ --- is the fluctuating number of open channels at moment $t$ due
to odor molecules bound with $R$s;
$g_{R}$ --- is the conductance of a single open channel.

A fast, very efficient method is developed for generating stochastic trajectories $n(t)$ and solving Eq. (1) numerically, see Fig. 2. The first, introductory simulations based on this method, [4], support the conclusion made in [1] and before, that ORN's selectivity can be much better than that of its receptors R, provided that odors are presented in low concentrations.

Figure 2: An example of realization of stochastic process n(t) and corresponding membrane voltage, with three spikes emitted. Here, the total number of R per the ORN is $N = 2.5 · 10^6$

[1] A. K. Vidybida, ``Maximization of the olfactory receptor neuron selectivity in
the sub-threshold regime'', Ukrainian Journal of Physics, vol. 68, no.4, p. 266, 2023. Available: {\tt https://doi.org/10.15407/ujpe68.4.266}

[2] K. Sato, M. Pellegrino, T. Nakagawa, T. Nakagawa, L. B. Vosshall, and
K. Touhara, ``Insect olfactory receptors are heteromeric ligand-gated ion
channels'', Nature, vol. 452, no. 7190, pp. 1002--1006, 2008. Available: {\tt https://doi.org/10.1038/nature06850}

[3] D. Wicher, F. Miazzi, ``Functional properties of insect olfactory receptors: ionotropic receptors and odorant receptors'', Cell and Tissue Research, vol. 383(1):7-19 (2021). Available: {\tt https://doi.org/10.1007/s00441-020-03363-x}

[4] A. Vidybida, "Selectivity Gain in Olfactory Receptor Neuron at Optimal Odor Concentration," 2024 IEEE International Symposium on Olfaction and Electronic Nose (ISOEN), Grapevine, TX, USA, 2024, pp. 1-3. Available: {\tt https://ieeexplore.ieee.org/document/10556323}

Speaker: Oleksandr Vidybida (Bogolyubov Institute for Theoretical Physics)

vidybida1.png

vidybida2.png

11:40 Development and analysis of novel integrable nonlinear dynamical systems on quasi-one-dimensional lattices. Parametrically driven nonlinear system of pseudo-excitations on a two-leg ladder lattice

Following the main principles of developing the evolutionary nonlinear integrable systems on quasi-one-dimensional lattices we suggest the novel nonlinear integrable system of parametrically driven pseudo-excitations on a regular two-leg ladder lattice. The initial (prototype) form of the system is derivable in the framework of semi-discrete zero-curvature equation with the spectral and evolution operators specified by the properly organized 3×3 square matrices. Although the lowest conserved local densities found via the direct recursive method do not prompt us the algebraic structure of system's Hamiltonian function, but the heuristically substantiated search for the suitable two-stage transformation of prototype field functions to the physically motivated ones has allowed to disclose the physically meaningful nonlinear integrable system with time-dependent longitudinal and transverse inter-site coupling parameters. The time dependencies of inter-site coupling parameters in the transformed system are consistently de?ned in terms of the accompanying parametric driver formalized by the set of four homogeneous ordinary linear di?erential equations with the time-dependent coeficients. The physically meaningful parametrically driven nonlinear system permits its concise Hamiltonian formulation with the two pairs of field functions serving as the two pairs of canonically conjugated field amplitudes. The explicit example of oscillatory parametric drive is described in full mathematical details.

Speaker: Dr Oleksiy O. Vakhnenko (Bogolyubov Institute for Theoretical Physics)

12:00 Coffee break

12:30 Dynamics of correlations of many colliding particles

The talk provides an overview of some advances in the mathematical understanding of the nature of the dynamics of the correlations of many colliding particles. The fundamental equations of modern mathematical physics are studied, in particular the hierarchies of the evolution equations of many hard spheres and their asymptotic behavior described by kinetic nonlinear equations.

First, an approach to describing correlations in a system of colliding particles interacting as hard spheres is discussed, based on a hierarchy of equations for the evolution of a sequence of correlation functions that are cumulants of distribution functions, called the Lioville hierarchy. It is proven that the constructed dynamics of correlations underlie the description of the dynamics of both a finite and an infinite number of hard spheres obeying the BBGKY hierarchies for reduced (marginal) distribution functions or reduced correlation functions.

The structure of expansions representing non-perturbative solutions of the Cauchy problem for these hierarchies of evolution equations is formulated. It has been established that the concept of cumulants of the groups of operators of the Lioville equations underlies non-perturbative expansions of solutions to the hierarchies of fundamental equations describing the evolution of observables and of the state of many hard spheres, as well as forms the basis of the kinetic description of their collective behavior.

In the talk, we also consider a new approach to the problem of a rigorous description of kinetic evolution by means of reduced (marginal) observables governed by the dual BBGKY hierarchy. One of the advantages of the developed approach to the derivation of kinetic equations from the underlying dynamics of many particles is that it provides an opportunity to construct kinetic equations with initial correlations, in particular correlations characterizing the condensed states of a system, and to describe the processes of the propagation of initial correlations within suitable scaling limits.

References
[1] Gerasimenko V I and Gapyak I V 2023 Advances in theory of evolution equations of many colliding particles. Proc. Inst. Math. NASU 20 729–804 doi:10.3842/trim.v20n1.528
[2] Gerasimenko V I and Gapyak I V 2022 Propagation of correlations in a hard sphere system. J Stat. Phys. 189 2 doi:10.1007/s10955-022-02958-8
[3] Gerasimenko V I and Gapyak I V 2021 Boltzmann–Grad asymptotic behavior of collisional dynamics. Reviews in Math. Phys. 33 2130001 32 doi:10.1142/S0129055X21300016
[4] Gerasimenko V I and Gapyak I V 2019 Processes of creation and propagation
of correlations in large quantum particle system. In: Panorama of Contemporary Quantum Mechanics – Concepts and Applications. London: InTech, 2019 doi:10.5772/intechopen.82836

Speaker: Prof. Viktor Gerasimenko (Institute of Mathematics NAS of Ukraine)

12:50 Kinetic model of the formation of STM-induced electrofluorochromism in molecular junctions

Experimental data on STM-induced electroluminescence in monomolecular junctions have led to the need to elucidate the physics of the formation of optoelectronic processes at the atomic-molecular level, taking into account both dynamic and relaxation processes. A mechanism for the formation of electrofluorochromism based on a kinetic model has been proposed [1]. In this model, the description of the optoelectronic process in a photoactive molecular junction takes into account the fact that the formation of electron current and electroluminescence (EL) is controlled not only by the shift of the orbital energies of the molecule relative to the Fermi levels of both electrodes, but also by the probability of the realization of many-body states of the molecule at different values and polarities of the bias voltage. Therefore, when current and EL are generated, the electronic states of charged forms of fluorophore molecules can act not only as mediators of electron transfer, but also become responsible for electrofluorochromism. It became clear that the EL in a molecular junction reflects the light emission of a fluorophore molecule not only between the singlet states of a neutral molecule, but also between the states of its charged forms. Thus, we show that electron transfer occurs through the transmission channels associated with electronic states of the neutral molecule and its cationic and anionic forms, which, at a definite bias voltages, are involved in electron transfer. The occupancies of these states are determined by kinetic processes in the molecular junction and therefore depend on the ratio of charge exchange rates between the molecule and the electrodes, the rates of non-radiative intramolecular transitions caused by inelastic interelectrode tunneling of electrons, as well as the rates of intramolecular radiative transitions enhanced by the plasmonic response. Analytical results are obtained using the tight-binding Hamiltonian for a molecule. The kinetic model made it possible to explain the features of EL in a monomolecular junction with the ZnPc fluorophore. Thus, it was shown that the description of EL based on the kinetic approach can serve as an effective tool for understanding the physics of optoelectronic processes in single-molecule structures.

1. E.Petrov, O.Kapitanchuk, Ye.Shevchenko, V.Gorbach, A.Lyubchik, Phys. Chem. Chem. Phys., 2024, DOI: 10.1039/d4cp01328j

Speaker: Oleksiy Kapitanchuk (Bogolyubov Institute for Theoretical Physics, National Academy of Sciences of Ukraine)

13:10 Polarization mechanism of bacteria motion in aquatic media

A new mechanism is proposed to explain the reasons for the bacteria's motion in the aquatic environment. The mathematical model of this mechanism is based on the hydrodynamic equations of active matter and takes into account the dynamics of the environment polarization and polarization of individual bacteria. It is assumed that the flow of light and the active motion of dielectric regions with different refractive indices inside the bacterium lead to the formation of a nonuniform distribution of dipole moments at the interface between the bacterium and the aqueous medium. This distribution is nonequilibrium and evolves along the bacterium and rotates. The interaction of this distribution with the environment due to surface deformation or due to ponderomotive force leads to the bacteria's motion. Such a motion can be represented as a type of turbine effect without attachment or as an interaction of the polarization current with a change in the local polarization of the medium. This mechanism differs significantly from the flagella motion mechanism and can explain the motility of flagellate bacteria. In addition, such a mechanism depends on the concentration of charged particles in the medium. Namely, with an increase in their concentration, the polarized region motion increases, which creates a greater bacterial surface deformation and causes a redistribution of polarization. Moreover, the collective bacteria motion can cause water mixing.

Speaker: Dr Oleksandr Cherniak (Bogolyubov Institute for Theoretical Physics)

13:30 → 14:30 Lunch

14:30 → 16:50 Afternoon Session 3

14:30 Towards relations between compaction and compressibility of hard sphere mixtures

The study of the influence of local properties of multi-particle conglomerations on their macroscopic properties is one among of the traditionally relevant problems of statistical physics. Parameterization of local properties can be carried out in various ways, for example, in terms of ordering parameter tensors, Euler invariants, Voronoi tessellations and others. While the macroscopic properties discussed above are the usual ones in statistical physics and thermodynamics, like compressibility, heat capacity, thermal conductivity, and others. In this paper, we study the influence of the compaction factor (packing) on the property of compressibility using the example of a model conglomeration of solid spheres, starting with a mono-disperse system and further, for multi-component mixtures. Using the known equations of state of the Carnahan-Starling type and their generalizations to the case of poly-disperse mixtures, the inverse problem of the influence of the proper parameters of the system (mixture) on the degree of compaction (packing) is considered. Non-monotonicity in the behavior of the packing parameter and the possibility of achieving its maximum value using a consistent selection of relations of the sizes of components and their molar fractions are shown. Application of the above-described approach to two different physical systems - a binary liquid mixture and a two-component granular system - showed quite good agreement between theory and experiment (especially in the case of a granular system). The proposed approach can be generalized without fundamental difficulties to the case of multi-particle conglomerations with an arbitrary number of components.

Speaker: Prof. Oleg Gerasymov (Odesa Mechnikov National University )

14:50 Elastic form factors of light alpha-cluster nuclei

Within the α-particle model, the structure of $^{12}C$, $^{16}O$, and $^{20}Ne$ nuclei is studied. With the use of the variational method with Gaussian basis, the wave functions are found for three-, four-, and five-particle systems consisting from α-particles. The charge density distributions and elastic form factors of $^{12}C$, $^{16}O$, and $^{20}Ne$ nuclei are calculated within the Helm approximation.

Speaker: Borys Grinyuk (Bogolyubov Institute for Theoretical Physics)

15:10 Pauli resonances in single- and many-channel systems

In this report, we present results of systematic investigations of peculiarities of redundant solutions of the resonating group method (RGM), which are known as the Pauli resonance states. Such resonance states appear when one tries to use more advanced (more precise) wave functions describing internal structure of interacting clusters. It is generally recognized that the Pauli resonance states are spurious solutions which blur real physical quantities such as phase shifts, cross sections. Their appearance cannot be attributed to enlarging of centrifugal and Coulomb barriers, they also appear in a single-channel approximation and thus the Pauli resonance cannot be considered as the Feshbach resonances.
The subject of our investigations is continuos spectrum states of light nuclei $^{6}$Li, $^{7}$Li, $^{8}$Be, $^{9}$Be and $^{10}$B, which are considered as two-cluster systems. Special attention is paid to the Pauli resonance states which appear in interaction of $^{6}$Li with neutrons, deuterons, tritons and alpha particles. All investigations are carried out in a three-cluster microscopic model, which was formulated in Ref. [1]. In this model dominant three-cluster configuration is transformed into a set of binary channels. One of the constituents of the binary channel is considered as a two-cluster subsystem. Spectrum of bound states and corresponding wave functions of the subsystem are obtained by solving the two-cluster Schrödinger equation. This allows us to use more adequate wave functions describing the internal structure of the two-cluster subsystem. This is rather important for two-cluster subsystems with a small separation energy, such as deuteron, $^{6}$Li and so on. Within the model, Gaussian functions are used to describe relative motion of clusters in bound states of a two-cluster subsystem and oscillator functions are utilized to expand wave function of continuous spectrum states of compound nucleus. At the first stage of our investigation, we use single-channel approximation in order to detect and analyze the Pauli resonance states.
It is found that the Pauli resonance states in selected nuclei lie in the energy range between 11 and 45 MeV, and their widths are varied from 8 keV to 8 MeV. The most dense area of resonance states are concentrated in the interval 16 < E<21 MeV. Two dense area of widths of resonance states are located in intervals 0.008<$\Gamma$<0.22 MeV and 0.9<$\Gamma$<1.2 MeV. In many cases only one Pauli resonance state appeared in a binary channel. We also determined several cases with two resonance states. It was demonstrated, the number of the Pauli resonance states are correlated with number of the Pauli forbidden states in a simple version of the RGM, when simple functions of the many-particle shell-model are employed for describing internal motion of nucleons within each cluster.
We also investigate properties of the Pauli resonances in a many-channel model of $^{6}$Li. This nucleus is studied within a three-cluster model which involves two three-cluster configurations $\alpha+p+n$ and $t+d+p$. These cluster configurations allowed us to take into account all dominant binary decay channels of the nucleus. It is shown that the Pauli resonances are observed in the $\alpha+d$, $^{5}$He+$p$, $^{5}$Li+$n$, $^{3}$He+$t$ channels when they are treated separately. When channels are coupled, the Pauli resonances migrate from one to another channel and substantially change their energy and width. We demonstrated how Pauli resonances in single- and many-channel systems can be effectively eliminated with minimal effects on the ground and shape resonance states.

References

[1] V. S. Vasilevsky, F. Arickx, J. Broeckhove, and T. P. Kovalenko, “A microscopic three-cluster model with nuclear polarization applied to the resonances of $^{7}$Be and the reaction $^{6}$Li($p$,$^{3}$He)$^{4}$He,” Nucl. Phys. A, vol. 824, pp. 37–57, 2009.

Speaker: Dr Victor Vasilevsky (Bogolyubov Institute for Theoretical Physics)

15:30 Coffee break

15:50 Initial value problem in the case of multivalued dispersion equations

Dispersion equations and relations are the key subjects of linear theories involving waves and collective excitations. However, in some systems, dispersion equations contain multivalued functions and their solutions are ambiguous. To resolve such uncertainty we suggest analyzing the initial value problem that gives the unambiguous solution.
As an example, we considered the excitation of the Dirac plasmons in graphene on a polar substrate and analyzed a strong coupling between plasmons in graphene and surface optical phonons of the substrate. Due to square-root singularity in graphene polarizability [1], the dispersion equation for this system contains branch points on the plane of complex frequency, $\omega$. The use of the initial value problem gives a unique solution and clarifies the physical picture of coupled oscillations. Particularly, we found that lower plasmon-phonon mode, which in terms of dispersion can have a good quality factor, is almost absent in excitation spectra. The main physical reason for the mode collapse is the suppression of space-time-dependent electric fields near $\omega=v_F k$, where $v_F$ is the Fermi velocity and $k$ is the plasmon wavenumber [2]. The evidence of the collapse can be seen in the relevant experiments [3, 4].

[1] S. M. Kukhtaruk and V. A. Kochelap, Phys. Rev. B 92, 041409(R) (2015).
[2] S. M. Kukhtaruk, V. A. Kochelap, V. N. Sokolov, K. W. Kim, Physica E: Low-dimensional Systems and Nanostructures, 79, 26, (2016).
[3] R. J. Koch, T. Haensel, S. I.-U. Ahmed, Th. Seyller, and J. A. Schaefer, Phys. Status Solidi C 7, 394 (2010).
[4] R. J. Koch, Th. Seyller, and J. A. Schaefer, Phys. Rev. B 82, 201413(R) (2010).

Speaker: Serhii Kukhtaruk (V. E. Lashkaryov Institute of Semiconductor Physics NAS of Ukraine)

16:10 Milky Way globular clusters in cosmological timescale. Probability of the interaction with the Galactic center

The main idea of the work is to carry out the dynamic evolution of the orbits of Globular Cluster (GC) subsystems sample lookback time up to 10 Gyr. This allows us to estimate the possibility of GCs interaction with the Galactic center that dynamically changed in the past. To reproduce the structure of the Galaxy in time, we used external potentials which dynamically changed in a past and now their characteristics are similar to the physical values of the Milky Way at the present day (mass and size of disk and halo). External potentials were selected from the large-scale cosmological database IllustrisTNG-100 (TNG-TVP). In these potentials, we reproduced the orbits of 147 GCs from Gaia DR3 in 10 Gyr lookback time using our own high-order N-body parallel dynamic code phi-GPU code. To identify clusters that have interaction with the Galactic center, we used the criteria of relative distance: it must be less than 100 pc. Applying this simple criteria, we obtained statistically significant rates of close passages of the GCs with the Galactic center. We identified ten GCs, including NGC 6401, Pal 6, NGC 6681, NGC 6712, NGC 6287, NGC 6642, NGC 6981, HP 1, NGC 1904, and NGC 362, with a high probability of close passages near the Galactic center in all four TNG-TVPs, particularly the first six with a probability of around 100%.

Speaker: Marina Ishchenko (MAO NAS Ukraine, 2 Fesenkov Astrophysical Institute, Observatory 23, 050020 Almaty, Kazakhstan 3 Nicolaus Copernicus Astronomical Centre Polish Academy of Sciences, ul. Bartycka 18, 00-716 Warsaw, Poland)

16:30 Orbital perturbation theory in Schwarzschild space-time

In our work, we obtain a set of Gaussian orbital perturbation equations in the Schwarzschild space-time in terms of Weierstrass elliptic functions, and solve it for several external forces in linear approximation. We consider forces defined from: the cosmological constant in the Schwarzschild–de Sitter space-time, various quantum gravity corrections, angular momentum from the Kerr space-time and some others. From this we obtain several observables, in particular, we consider a simple "kludge" scheme for gravitational waveforms.

Speaker: Oleksii Yanchyshen (Bogolyubov Institute for Theoretical Physics)