Excitable membrane of olfactory receptor neuron (ORN) is populated with up to several millions of identical receptor proteins (R) able to bind / release odor (O) molecules. The affinity of R to O depends on the odor presented, and this is the initial mechanism which is recuired for the olfactory selectivity to exist.
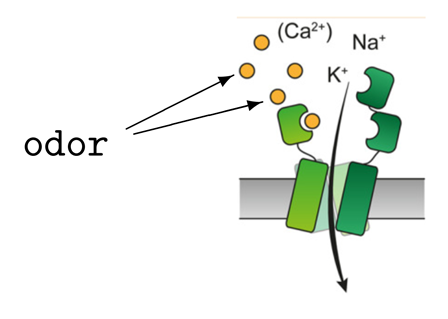
Figure 1: Simplified R structure. Modified from [3].
The affinity of R to O depends on the odor presented, and this is the very first step the olfactory selectivity builds up. Recently, [1], it was shown for a so called membrane-less ORN model that its selectivity can be much better than that of its R. A more realistic ORN model should include an excitable membrane with its electric transients. This introduces time parameter into the ORN's response to stimulation. The latter renders inappropriate used in [1] reasoning in terms of binomial distribution, and necessitates consideration of temporal properties of O binding-releasing and the membrane charging-discharging-firing.
In this contribution, we develop an approach in which the number of R bound with O $n(t)$, is modeled as a Markov stochastic process. With each bound R,
as it is observed for insects [2], Fig. 1, we associate an open channel having conductance 0.015 nS, which injects a depolarizing current through the membrane.
The futher membrane evolution is governed by the leaky integrate-and-fire neuronal model, see Eq. (1).
$c_M\frac{dV(t)}{dt}=-g_l(V(t)-V_{rest}) - n(t)g_{R}(V(t)-V_{e})$,
where $V(t)$ --- is the membrane voltage; $V_{rest}$ --- is the resting voltage;
$c_M$ --- is the total capacity of ORN's membrane;
$g_l$ --- is the total leakage through it;
$V_{e}$ --- is the reversal potential for current through open $R$;
$n(t)$ --- is the fluctuating number of open channels at moment $t$ due
to odor molecules bound with $R$s;
$g_{R}$ --- is the conductance of a single open channel.
A fast, very efficient method is developed for generating stochastic trajectories $n(t)$ and solving Eq. (1) numerically, see Fig. 2. The first, introductory simulations based on this method, [4], support the conclusion made in [1] and before, that ORN's selectivity can be much better than that of its receptors R, provided that odors are presented in low concentrations.

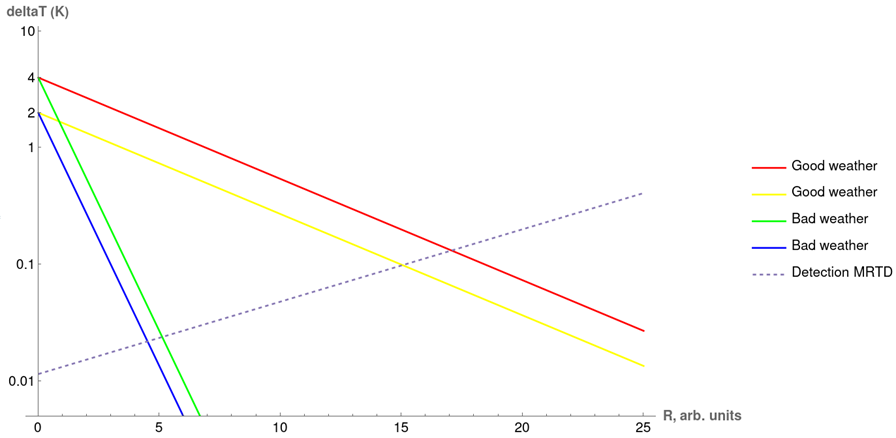
Figure 2: An example of realization of stochastic process n(t) and corresponding membrane voltage, with three spikes emitted. Here, the total number of R per the ORN is $N = 2.5 · 10^6$
[1] A. K. Vidybida, ``Maximization of the olfactory receptor neuron selectivity in
the sub-threshold regime'', Ukrainian Journal of Physics, vol. 68, no.4, p. 266, 2023. Available: {\tt https://doi.org/10.15407/ujpe68.4.266}
[2] K. Sato, M. Pellegrino, T. Nakagawa, T. Nakagawa, L. B. Vosshall, and
K. Touhara, ``Insect olfactory receptors are heteromeric ligand-gated ion
channels'', Nature, vol. 452, no. 7190, pp. 1002--1006, 2008. Available: {\tt https://doi.org/10.1038/nature06850}
[3] D. Wicher, F. Miazzi, ``Functional properties of insect olfactory receptors: ionotropic receptors and odorant receptors'', Cell and Tissue Research, vol. 383(1):7-19 (2021). Available: {\tt https://doi.org/10.1007/s00441-020-03363-x}
[4] A. Vidybida, "Selectivity Gain in Olfactory Receptor Neuron at Optimal Odor Concentration," 2024 IEEE International Symposium on Olfaction and Electronic Nose (ISOEN), Grapevine, TX, USA, 2024, pp. 1-3. Available: {\tt https://ieeexplore.ieee.org/document/10556323}