XI Conference of Young Scientists "Problems of Theoretical Physics"
Online meeting
TOPICS OF THE CONFERENCE
High energy physics, astroparticle physics, quantum cosmology, theory of nuclear systems, quantum field theory, theory of symmetries, theory of nonlinear processes in macromolecular structures, nanosystems and plasmas, dynamics of open strongly nonequilibrium physical, biological, economic and information systems.
SECTIONS
- Astrophysics and Cosmology
- Mathematical Physics
- Statistical Theory of Many-body Systems
- Physics of Biological Macromolecules
- Condensed Matter Physics
- Physics of Nuclei and Elementary Particles
The lectures of leading scientists will be presented in each section.
INVITED LECTURERS
Prof. Horst Stöcker (FIAS, Germany)
Prof. Oleg Lavrentovich (LCI, USA)
Prof. Andrey Varlamov (SPIN-CNR, Italy)
Prof. Francesca Mocci (UniCa, Italy)
Prof. Yuriy Izotov (BITP, Ukraine)
Prof. Sergej Volkov (BITP, Ukraine)
We invite the undergraduate and postgraduate students and the young scientists. Maximum age of a participant is 35. Working language of the Conference is English. We provide 20 min for an oral talk. Proceedings of the best talks will be recommended for publishing in the Ukrainian Journal of Physics.
ORGANIZING COMMITTEE
Head – Academician of NAS of Ukraine, Prof Dr. Anatoly Zagorodny;
Ph.D. Ivan Starodub; Ph.D. Volodymyr Kravchuk; Ph.D. Sergiy Perepelytsya; Denys Savchenko; Anton Rudakovskyi; Ph.D. Oleksiy Zdorevskiy
-
-
10:00
→
10:05
Opening of the Conference
-
10:05
→
13:30
Physics of Nuclei and Elementary Particles
-
10:05
The equation of state of hot dense qcd- matter, gravitational waves and collective flows 45mSpeaker: Prof. Horst Stöcker (FIAS Goethe Universitaet Frankfurt GSI)
-
10:50
Connecting fluctuation measurements in heavy ion collisions and grand canonical susceptibilities: global conservation effects 20m
We present the relation between cumulants of a conserved charge measured in a subvolume of a thermal system and the corresponding grand-canonical susceptibilities, taking into account exact global conservation of all QCD charges. The derivation is presented for an arbitrary equation of state, with the assumption that the subvolume is sufficiently large to be close to the thermodynamic limit. Our framework – the subensemble acceptance method (SAM) – quantifies the effect of global conservation laws and is an important step toward a direct comparison between cumulants of conserved charges measured in central heavy ion collisions and theoretical calculations of grand-canonical susceptibilities, such as lattice QCD. We show that the global conservation effects cancel out in any ratio of two second order cumulants, in any ratio of two third order cumulants, as well as in a ratio of strongly intensive measures Σ and ∆ involving any two conserved charges, making all these quantities particularly suitable for theory-to-experiment comparisons in heavy-ion collisions. We also show that the same cancellation occurs in correlators of a conserved charge, like the electric charge, with any non-conserved quantity such as net proton or net kaon number. The main results of the SAM are illustrated in the framework of the hadron resonance gas model. We also elucidate how net-proton and net-Λ fluctuations are affected by conservation of electric charge and strangeness in addition to baryon number.
Speaker: Roman Poberezhnyuk (Bogolyubov Institute for Theoretical Physics of the National Academy of Sciences of Ukraine) -
11:10
Equation of State at Finite Baryon Density and External Magnetic Field from Lattice QCD 20m
The report is devoted to lattice study of QCD equation of state (EoS) at finite baryon chemical potential and nonzero external magnetic field. The simulations are performed with rooted dynamical staggered $u$, $d$, and $s$ quarks at physical quark masses. In view of the sign problem, the study is carried out at imaginary chemical potential. The results are analytically continued to real chemical potential domain. We present our preliminary results for pressure computed for various values of temperature and magnetic field.
Speaker: Natalia Kolomoyets (JINR) -
11:30
Bose-Einstein condensation phenomenology in systems with repulsive interactions 20m
The role of repulsive interactions in statistical systems of Bose particles is investigated. Three different phenomenological frameworks are considered: a mean field model, an excluded volume model, and a model with a medium dependent effective mass. All three models are tuned to yield similar equations of state, with only minor deviations from the ideal Bose gas at small chemical potentials. Our analysis indicates, however, that these models lead to qualitatively different results for the Bose-Einstein condensation phenomenon. We discuss the different aspects of this phenomenon, namely, an onset of the Bose-Einstein condensation, particle number fluctuations, and a behavior of the Bose condensate. The obtained results can be helpful for interpreting the lattice QCD data at small temperature and large isospin chemical potential and the data on multiple pion production in high energy nuclear collisions.
Speaker: Mr Oleh Savchuk (Frankfurt Institute For Advanced Studies) -
11:50
Coffee break 20m
-
12:10
Revisiting the Polyakov loop Nambu-Jona-Lasonio model at finite density of baryon charge 20m
We revisit the Polyakov Loop coupled Nambu-Jona-Lasinio model that maintains the Polyakov loop dynamics at zero temperature, which is the most interesting for astrophysical applications. For this purpose we re-examine potential for the deconfinement order parameter at finite baryonic densities. Secondly, and the most important, we explicitly demonstrate that naive modification of this potential at any temperature is formally equivalent to assigning a baryonic charge to gluons. We develop a general formulation of the present model which is free of the discussed defect and is normalized to asymptotic of the QCD equation of state given by $\mathcal{O}(\alpha_s^2)$ perturbative results. We also demonstrate that incorporation of the Polyakov loop dynamics to the present model sizably stiffens the quark matter equation of state supporting an existence of heavy compact stars with quark cores.
Speaker: Oleksii Ivanytskyi (Bogolyubov Institute for Theoretical Physics) -
12:30
Femtoscopic analysis of relativistic heavy-ion collisions in the hydrokinetic approach 20m
The theoretical description of the femtoscopy scales in ultrarelativistic heavy-ion collisions at different energies and for different colliding ion pairs (Au + Au collisions at the top RHIC energy $\sqrt{s_{NN}}=200$ GeV, Pb + Pb collisions at the LHC energies $\sqrt{s_{NN}}=2.76$ and $\sqrt{s_{NN}}=5.02$ TeV, the LHC Xe + Xe collisions at $\sqrt{s_{NN}}=5.44$ TeV) is provided within the integrated HydroKinetic model (iHKM). The comparison of the model simulation results, obtained for the considered collision types at the similar values of the mean charged particle multiplicity ⟨$dNch/dη$⟩ shows that the magnitudes of the corresponding interferometry radii depend not only on ⟨$dNch/dη$⟩ but also on the geometric sizes of the colliding nuclei.
Speaker: Musfer Adzhymambetov (Bogolyubov Institute for Theoretical Physics) -
12:50
Production of HNL in 3-body decays of mesons. Comparison with PYTHIA approach 20m
The Standard Model (SM) is a particle physics theory that is consistent up to very high energy scales and verified in numerous experiments up to $\sim 14$ TeV. However, it fails to explain some phenomena such as massiveness of neutrinos, dark matter, dark energy, baryon asymmetry of the Universe etc. Therefore SM is incomplete and requires an extension.
One possible approach is by adding new particles to the theory. There are two possible answers to the question "Why do we not observe particles of new physics in experiments?" The first answer is the following. The new particles are very heavy and can not be produced in modern accelerators like LHC. To detect them one has to build more powerful and more expensive accelerators. There is another possibility. The particles of new physics can be light particles that feebly interact with SM particles.
The last case is very interesting for the experimental search of the new physics in the intensity frontier experiments just now. There are different choices of new renormalized interaction Lagrangian of particles of new physics with SM particles. It's called portals.In this paper, we consider a heavy neutral lepton (HNL) portal. The phenomenology of GeV-scale HNL was considered in details in [1]. We will compare the analytical results for HNL production in 3-body decays of mesons with PYTHIA approximation.
The simplest way of neutrino modification of the SM involves extension of the SM by neutrino singlets with right chirality (in the SM all right-handed fermions are singlets), which extremely faintly interact with SM particles. Such neutrinos are called sterile neutrinos or heavy neutral leptons. Renormalized and gauge-invariant interaction of new neutrinos with the SM particles is similar to the Yukawa interaction of left-handed quarks doublets with singlets of the right-handed quarks, namely:
$$ \mathcal L_{int}=-\left(F_{\alpha I}\bar L_\alpha \tilde H N_I+h.c.\right), $$ where $\alpha=e,\mu,\tau$, index $I$ is from 1 to full number of the sterile neutrinos, $L_{\alpha}$ – doublet of leptons of $\alpha$-generation, $N_I$ – right-handed sterile neutrino, $F_{\alpha
I}$ – new matrix of dimensionless Yukawa couplings, ${\tilde H}=i\sigma_2H^\star$. Taking the low energy limit and considering sterile neutrino as Majorana particles, we can write full Lagrangian of the modified neutrino sector of the SM $$ \mathcal{L}_{\nu,N}=i \bar{\nu_k} \not\partial \nu_k + i \bar{N_I} \not\partial N_I - \left( F_{\alpha I}\bar{\nu}_{\alpha} N_I + \frac{M_{I}}{2} \bar{N_I}^c N_I + h.c. \right), $$ where $M_I$ – Majorana mass terms. As a result of the neutrino states mixture, the active neutrino states become superposition of the mass states of the active and the sterile neutrinos. It means that sterile neutrinos interact with SM particles similarly to active neutrinos: $$ \mathcal{L}_{int} = -\biggl(\frac{g}{2\sqrt 2} W^+_\mu\!\sum_{I,\alpha} \overline{N^c}_I U_{I\alpha} \gamma^\mu (1-\gamma_5) \ell^-_\alpha + \frac{g}{4 \cos\theta_W}Z_\mu\! \sum_{I,\alpha}\overline{N^c}_I U_{I\alpha} \gamma^\mu (1-\gamma_5) \nu_\alpha + h.c.\biggr), $$ where $U_{I\alpha}=F_{I\alpha}/M_I$ is so called mixing angle. For intensity frontier experiment it is very important to built sensitivity region. It is a region in space of parameters of new particle (mass and coupling), when particle can be detected in the experiment. To build it one has to solve inequality $N_{HNL}^{reg}>N_0$, where $N_0$ is minimal expected number of new particle for successful of experiment, $N_{HNL}^{reg}$ is number of HNL that can be detected: $$ N_{HNL}^{reg}\simeq N^{produced}_{HNL} P_{geom} P_{decay}. $$ Here $N_{HNL}^{produced}$ is number of the produced \textit{HNL}-particles, $P_{geom}$ is a probability of the produced HNL-particles to move towards the detector, $P_{decay}$ is a probability of the produced HNL-particles to decay in the volume of the vacuum tank before the detectors. For approximate calculations of the sensitivity region, PYTHIA is often used. It is a widely used program for the generation of high-energy physics events. PYTHIA is good for generation of 2-body mesons' decay, but for HNL production it is important to take into account 3-body decay too. PYTHIA uses predefined matrix element to generate 3-body semileptonic decays of $B$ and $D$ mesons correspondingly $$ \overline{|M_{fi}|^2_B} = (p_h\,p_\nu) (p_{h^\prime} \, p_\ell),\quad \overline{|M_{fi}|^2_D} = (p_h\,p_\ell) (p_{h^\prime} \, p_\nu). $$ It does not contain mesons' form-factors and its matrix elements obviously differs from correct matrix elements for HNL production in 3-body mesons' decay. The goal of the project is to estimate the importance of this uncertainty for construction of sensitivity region to HNL. We considered in details probability density function for the energy of the HNL-particles $pdf(E_N)$, $P_{geom}$ and $P_{decay}$ and make following conclusions.- Computations of 3-body decay of $\tau$-lepton with HNL production in Pythia coincide with correct computations.
- For description of reactions of pseudoscalar meson 3-body decay into another pseudoscalar meson ($B^- \rightarrow D^0 +\ell^- + N$ and $D^- \rightarrow K^0 +\ell^- + N$) the matrix elements of type $B$ in Pythia is better to use
- For description of reactions of pseudoscalar meson 3-body decay into another vector meson ($B^- \rightarrow D^\star(2007)^0 +\ell^- + N$ and $D^- \rightarrow K^\star(892)+\ell^- + N$) the matrix elements of type $D$ in Pythia is better to use.
- Among the considered 3-body reactions, due to a suitable choice of PYTHIA matrix elements (type of $B$ and $D$), one can get the smallest difference with correct matrix element for reaction $B^- \rightarrow D^0 +e^- + N$ (difference $\sim 1\%$), while the largest unremovable difference is for reaction $D^- \rightarrow K^\star(892) +e^- + N$ (difference $\sim 5\%$).
[1] Kyrylo Bondarenko, Alexey Boyarsky, Dmitry Gorbunov, and Oleg Ruchayskiy. Phenomenology of GeV-scale Heavy Neutral Leptons. JHEP, 11:032, 2018.
Speaker: Yuliia Borysenkova (Taras Shevchenko National University of Kyiv) -
13:10
Phenomenology of GeV-scale Chern-Simons boson 20m
The Standard Model (SM) is a particle physics theory that is consistent up to very high energy scales and verified in numerous experiments up to $\sim 14$ TeV. However, it fails to explain some phenomena such as massiveness of neutrinos, dark matter, dark energy, baryon asymmetry of the Universe etc. Therefore, SM is incomplete and requires an extension.
One possible approach is by adding new particles to the theory. There are two possible answers to the question "Why do we not observe particles of new physics in experiments?" The first answer is the following. The new particles are very heavy and can not be produced in modern accelerators like LHC. To detect them one has to build more powerful and more expensive accelerators. There is another possibility. The particles of new physics can be light particles that feebly interact with SM particles.
The last case is very interesting for the experimental search of the new physics just now. There are three possible choices of new renormalized interaction Lagrangian of particles of new physics with SM particles. It's called portals. There are scalar portal, heavy neutral leptons portal, vector portal. There are other portals of high-dimensional operators such as portal of pseudoscalar particles (axion-like particles), or Chern-Simons like (parity odd) interaction of electroweak gauge bosons with a new vector field [1].In this paper, we consider a Chern-Simons (CS) portal with new neutral vector particle ($X$) boson.
This extension has not yet been studied sufficiently. This interaction was proposed in [2]. It origins from non-trivial anomaly cancellations in theory with new heavy fermions. It has gauge-invariant form
$$ \mathcal{L}_1=\frac{C_Y}{\Lambda_Y^2}\cdot X_\mu (\mathfrak D_\nu H)^\dagger H B_{\lambda\rho} \cdot\epsilon^{\mu\nu\lambda\rho}+h.c., \quad \mathcal{L}_2=\frac{C_{SU(2)}}{\Lambda_{SU(2)}^2}\cdot X_\mu (\mathfrak D_\nu H)^\dagger F_{\lambda\rho} H\cdot\epsilon^{\mu\nu\lambda\rho}+h.c. $$ In the low energy limit (unitary gauge) the effective renormalized Lagrangian of three particle interaction CS boson with SM particles is $$ \mathcal{L}_{CS}=c_z \epsilon^{\mu\nu\lambda\rho} X_\mu Z_\nu \partial_\lambda Z_\rho +c_\gamma \epsilon^{\mu\nu\lambda\rho} X_\mu Z_\nu \partial_\lambda A_\rho+\left\{ c_w \epsilon^{\mu\nu\lambda\rho} X_\mu W_\nu^- \partial_\lambda W_\rho^+ + h.c.\right\}. $$ For the experimental search of the new particle, it is very important to theoretically consider channels of production and decay of the new particle. We consider the case of experiments on Cern SPS accelerator, where CS particles can not be produced from the decay of real $W$, $Z$ bosons. In this paper, we consider the production of CS GeV-scale particles in mesons' decay. To do it we get effective Lagrangian of CS interaction with different quarks due to presented here loop diagram in the form $$ \mathcal{L}_{CSd}= \sum_{m\neq n}\Theta_{1W}\left( C^d_{mn}\, \bar{\Psi}_{d_n}\, \gamma^{\mu}\,\hat P_L \, \Psi_{d_m} X_{\mu}+h.c.\right)%-\sum_n\Theta_W^1 g^2 C^d_{nn}\, \bar{\Psi}_{d_n}\, \gamma^{\mu}\,\hat P_L \, \Psi_{d_n} X_{\mu}, $$ where $\Theta_{1W}$ is real part of $c_w$ coupling and $C^d_{bs}=1.97\cdot 10^{-4}$, $C^d_{bd}=4.43\cdot 10^{-5}$, $C^d_{sd}=1.77\cdot 10^{-6}$. As it turned out the loop with different quarks does not suffer from divergence problem and we have to take into account only interaction with down quarks, because coefficients of interaction with up quarks are sufficiently smaller. So, we will consider CS particle production in meson's decay only due to decay of heavy down quark in the meson. Initial lightest mesons containing $b$ and $s$ quarks are $B$-mesons and $K^\pm$, $K^0_S$, $K^0_L$ mesons. Possible reaction of $B$-meson decay with $X$-particle production is decay into pseudoscalar mesons ($K$ and $\pi$ mesons), scalar mesons ($K^{0\star}(700)$, $K^{0\star}(1430)$), vector mesons ($K^\star(892)$, $K^\star(1410)$, $K^\star(1680)$), pseudovector mesons ($K_1(1270)$, $K_1(1400)$) and tensor final meson states ($K_2(1430)$). For the initial kaons states, the only possible 2-body decay is the process $K \to \pi +X$. There are 3 types of the kaons: $K^{\pm}$, $K^0_L$, $K^0_S$. Since $K^0_S$ is the $CP$-even eigenstate, the decay $K^0_S\to \pi S$ is proportional to the CKM $CP$-violating phase and is strongly suppressed. Further we assume that the corresponding branching ratio vanishes and consider only reactions $K^\pm \to \pi^\pm +X$ and $K^0_L \to \pi^0 +X$. The amplitude of $h$-meson decay into $h'$-meson and $X$-particle has the form $$ M_{h\rightarrow h'X}=\Theta_{1W} C^d_{mn} \, \langle h'(p'))|\bar d_n\gamma^{\mu} \hat P_L d_m|h(p)\rangle\, \epsilon^{\star\lambda_X}_{\mu}. $$ This quantity can be obtained with help of formalism summarised in [3]. In the following, we plan to complete consideration of the production of CS particles by examining direct CS production in $p-p$ collisions. Also, we plan to consider possible channels of CS particles' decay.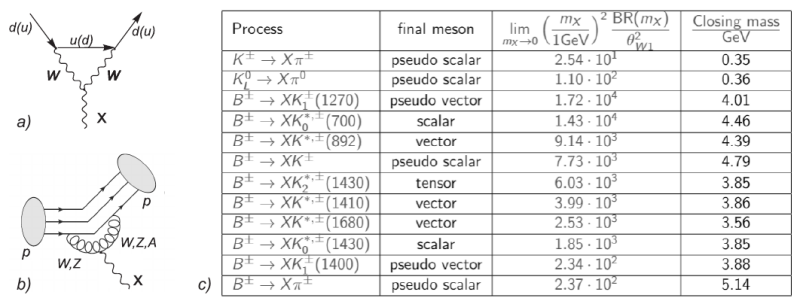 Figure 1. a) loop diagram of quarks interactions with CS particles; b) diagram of CS production in meson's decay c) decay of $B$- and $K$-mesons with CS production.
Figure 1. a) loop diagram of quarks interactions with CS particles; b) diagram of CS production in meson's decay c) decay of $B$- and $K$-mesons with CS production.[1] Sergey Alekhin et al. A facility to Search for Hidden Particles at the CERN SPS: the SHiP physics case. Rept. Prog. Phys., 79(12):124201, 2016.
[2] Ignatios Antoniadis, Alexey Boyarsky, Sam Espahbodi, Oleg Ruchayskiy, and James D.Wells. Anomaly driven signatures of new invisible physics at the Large Hadron Collider. Nucl. Phys., B824:296–313, 2010.
[3] Iryna Boiarska, Kyrylo Bondarenko, Alexey Boyarsky, Volodymyr Gorkavenko, Maksym Ovchynnikov, and Anastasia Sokolenko. Phenomenology of GeV-scale scalar portal. JHEP, 11:162, 2019.Speaker: Mariia Tsarenkova (Taras Shevchenko National University of Kyiv)
-
10:05
-
13:30
→
14:30
Lunch 1h
-
14:30
→
17:40
Condensed Matter Physics
-
14:30
Thermoelectricity: from the iron arc of the epoch of Alessandro Volta to ferrofluids today 45m
I will start my talk with the review of the exciting story of thermoelectricity in which were involved such famous scientists as Luigi Galvani, Alessandro Volta, Thomas Seebeck, Jean Charles Athanase Peltier, Walter Nernst, William Tompson, Nevil Mott, Lars Onsager, philosopher Georg Wilhelm Hegel, political figures like Napoléon Bonaparte.
Then I will pass to the main concepts of thermodynamic and kinetic approaches to the description of thermoelectric and thermomagnetic phenomena, will discuss the cases of their giant manifestation. I will formulate the requirements for the materials necessary for practical applications of thermoelectricity and present already available new materials.
In the final part of my talk I will shortly present the Future Emergent Technologies European Project MAGENTA - MAGnetic nanoparticle based ENergy materials for Thermoelectric device Applications (CEA – CNR – FIAT-DEMOCRITOS – …. ).
Speaker: Prof. Andrey Varlamov (Istituto superconduttori, materiali innovativi e dispositivi (SPIN-CNR)) -
15:15
Coulomb and vibration effects in spin-polarized current through a single-molecule transistor 20m
In recent years nanoscale transistors gain more scientific interest. The single-molecule transistor, where vibrating molecule is placed between two massive electrodes, appears to be a challenging device for further fundamental study and application in electronics. In this device along with the possibility of elastic tunneling the electrons can tunnel inelastically, emitting or absorbing vibrons. New transport phenomena also occur while the current of spin-polarized carriers through molecular transistor is controlled by an external magnetic field, providing an application in spintronics.
The current through spintronic molecular transistor in an external magnetic field is studied. We consider a molecule placed between electrodes, which are fully spin-polarized in opposite directions. The electron-vibron interaction and the Coulomb correlations in the system are taken into account. It is known that the dependence of the current on bias voltage in molecular transistors at low temperatures have form of step-like function (see e.g. [1]). Current jumps (Franck-Condon steps) occur, when new inelastic tunnel channels open.

Fig.1: The dependence of current on bias voltage $I(V)/I_0$ for spintronic molecular transistor at low temperatures for different values of Coulomb interaction (solid thin curve corresponds to negligibly small Coulomb interaction). $I_0=e\Gamma/(2\hbar)$, where $\Gamma$ is the tunneling level width. The bias voltage in energy units is normalized to molecule’s vibration quantum.The average current has been found using the density matrix method in perturbation theory over tunnel coupling. It has been obtained that the current dependences in our model have doubled number of Franck-Condon steps (Fig. 1) compared to an “ordinary” molecular transistor. The doubling is due to the appearance of second elastic channel in the system with Zeeman splitting. It has been revealed that for strong Coulomb interaction the heights of Frank-Condon steps are suppressed (solid thick, dotted and dashed curves, Fig. 1) and the regions without steps on the current-voltage characteristics appear (dotted and dashed curves, Fig. 1). The effects are caused by interplay of Franck-Condon and Coulomb blockade lifting by bias voltage. It has been also shown that the lifting of the Coulomb blockade in the Zeeman split system procceds in stages. It has been obtained that the temperature dependence of a conductance of spintronic molecular transistor for strong electron-vibron interaction is anomalously nonmonotonic in the region of intermediate temperatures in a wide range of external magnetic fields and at arbitrary Coulomb energy.
The results lead to a better understanding of the transfer of the current of interacting carriers in complex systems, allow one to interpret the data of tunnel experiments, provide background for engineering of nanoelectronic devices controlled by an external magnetic field.Speaker: Dr Anastasiia Shkop (B. Verkin Institute for Low Temperature Physics and Engineering of the NAS of Ukraine) -
15:35
Bending-induced flexoelectric polarization and conductivity of low-dimensional transition metal dichalcogenides 20m
Bulk TMDs are typically non-polar centrosymmetric semiconductors with a relatively wide band gap ~(1.1 – 2) eV [1], however, on transition from the bulk form to the nanoscale additional orderings emerge [2, 3]. The properties of low-dimensional (LD) transition metal dichalcogenides (TMDs) with a chemical formula MX2 (M – metal Mo, W, Re; X – chalcogen S, Se, Te) and Janus-compounds (JC) with a chemical formula MXY (X, Y – chalcogens) can be changing in a broad range of properties varying from non-polar to ferroelectric, and from direct-band semiconductor to metallic [4, 5]. These opportunities of tunability of polar and semiconducting properties are provided by controlling factors, such as composition, doping, and field effect. However, known studies in this fields are mostly empirical and almost not systematized.
Recently [6] we developed LGD-type theory for the description of polar phenomena in LD-TMDs, specifically explored flexoelectric origin of the polarization induced by a spontaneous bending and by inversion symmetry breaking due to the interactions with substrate. This work is devoted to the establishment of correlation between polar and electronic properties of LD-TMDs and JCs [7]. Using finite element modeling (FEM) we calculated the elastic and electric fields, flexoelectric polarization and free charge density for a TMD (or JC) nanoflake placed on a rough gold substrate with a sinusoidal profile of the corrugation.
Analysis of FEM results obtained for the different flake thickness (varying from 10 layers to 300 nm) and corrugation depth (varying from 0 to 50 nm), allows to corroborate the flexoelectric nature of the out-of-plane electric polarization and establish the unambiguous correlation between the polarization and static conductivity modulation caused by inhomogeneous elastic strains coupled with deformation potential and strain gradients, which evolve in the nanoflake due to the adhesion between the flake surface and corrugated substrate.
We revealed a pronounced maximum at the thickness dependences of the electron and hole conductivity of MoX2 and MXY nanoflakes placed on a substrate with a sinusoidal corrugation. Namely the conductivity is maximal for a (75 - 80) nm thick flakes placed on a gold substrate with the 4 nm corrugation height (see Fig. 1). This result opens the way for the nanoflakes geometry optimization towards significant improvement their polar and electronic properties, which necessary for their advanced applications in nanoelectronics and memory devices.The work has received funding from the National Research Foundation of Ukraine (Grant application 2020.02/0027, Contrast N 52/02.2020).
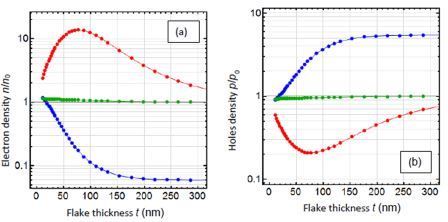
FIGURE 1. Thickness dependence of the bending-induced relative static electron (a), and holes (b)
conductivity at the top surface of a MoTe2 placed on a corrugated gold (Au) substrate. Nanoflake top
and bottom surfaces reaction when it is placed at the “top” of the corrugation are shown by red and
blue symbols, respectively; and the nanoflake top reaction when it is placed the at the corrugation
“slope” is shown by green curves. From [7].[1] S. Kang, S. Kim, S. Jeon, W.-S. Jang, D. Seol, Y.-M. Kim, J. Lee, H. Yang, and Y. Kim.
Atomic-scale symmetry breaking for out-of-plane piezoelectricity in two-dimensional transition
metal dichalcogenides. Nano Energy 58, 57-62 (2019).
[2] S. Yuan, X. Luo, H.L. Chan, C. Xiao, Y. Dai, M. Xie, and J. Hao. Room-temperature
ferroelectricity in MoTe2 down to the atomic monolayer limit. Nat. Commun. 10, 1775 (2019).
[3] K.-A.N. Duerloo, Y. Li, and E.J. Reed, Structural phase transitions in two-dimensional Mo- and
W-dichalcogenide monolayers, Nat. Commun. 5, 4214 (2014).
[4] D.W. Boukhvalov and M.I. Katsnelson. Enhancement of chemical activity in corrugated
graphene. J. Phys. Chem. C 113, 14176 (2009).
[5] S.V. Kalinin, and V. Meunier. Electronic flexoelectricity in low-dimensional systems. Phys.
Rev. B, 77, 033403 (2008).
[6] A.N. Morozovska, E.A. Eliseev, G.I. Dovbeshko, M.D. Glinchuk, Y. Kim, and S.V. Kalinin.
Flexo-induced ferroelectricity in low dimensional transition metal dichalcogenides. Phys. Rev. B
102, 075417 (2020).
[7] A. N. Morozovska, E. A. Eliseev, H. V. Shevliakova, G. I. Dovbeshko, M. D. Glinchuk, Y. Kim,
and S. V. Kalinin. Correlation between corrugation-induced flexoelectric polarization and
conductivity of low-dimensional transition metal dichalcogenides (http://arxiv.org/abs/2011.09326)Speaker: Ms Hanna Shevliakova (Department of Microelectronics, Igor Sikorsky Kyiv Polytechnic Institute) -
15:55
Influence of Mismatch Strain on Electrocaloric Properties of Core-Shell Ferroelectric Nanoparticles 20m
Ferroelectrics are among the most interesting objects for fundamental and applied studies of spontaneous polarization dynamics. Special efforts are intended to answer the question on how complex topological states such as flux-closure domains, polarization vortices, or skyrmions, which sometimes exist in nanosized ferroelectrics, can be controlled by elastic forces and/or electric fields.
Several authors [1-6] have studied numerically the electrocaloric effect (ECE) in ferroelectric nanoparticles using a phase field method combined with the Landau-Ginzburg-Devonshire (LGD) approach. These studies demonstrate the possibility to reveal a giant ECE in various ferroelectric nanoparticles, where the conditions for observing the effect are almost always determined in an empirical way, except for the case of single-domain nanoparticles [7]. Within the framework of the approach we explored the impact of the mismatch strain on ECE of core-shell ferroelectric nanoparticles with complex domain structure. We performed calculations for a multiaxial ferroelectric core covered with a paraelectric shell (see Fig. 1a), with or without mismatch strains. The latter are induced by the difference of the core and shell lattice constants. We studied the influence of the core radius on the electrocaloric cooling temperature and coercive field (see Fig. 1b). We revealed the significant asymmetry of the ferroelectric properties (transition temperature, polarization magnitude, coercive field) and ECE with respect to the sign of the mismatch strain. This result is in a qualitative agreement with experimental results of Barnakov et al. [8], who studied the ferroelectric properties of BaTiO3 nanocubes coated with metal carboxylates in two forms – one was crystalline and provided a lattice mismatch, and the other was non-crystalline without mismatch conditions. The revealed polar effects differed by many orders of magnitude for these two coatings. The analytical results obtained in this study can be used for the optimization of core-shell ferroelectric nanoparticle sizes for advanced applications in nanoelectronics and nano-coolers. Specifically, our results allow us to select optimal parameters to reach “giant” negative values of an electrocaloric response from an ensemble of non-interacting core-shell nanoparticles. A giant ECE, such as cooling by 20 K, could be very promising for advanced applications of ferroelectric nanocomposites in energy convertors and cooling systems.
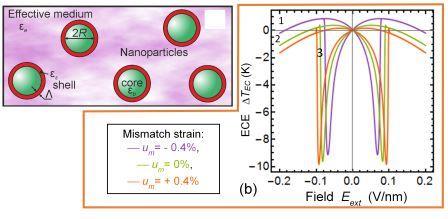
Figure 1. (a) Spherical ferroelectric NPs covered with a thin semiconducting shell and placed in an isotropic dielectric polymer (b) Dependence of the EC temperature change $\Delta T_EC$ on a quasi-static external electric field for nanoparticles with a $BaTiO_3$ core covered with a rigid shell $ε_s$=300. The curves are calculated for different values of mismatch strain between the core and shell $u_m$ = –0,4% (curve 1), 0 (curve 2), and +0.4% (curve 3). Shell thickness $\Lambda$ = 4 nm, and T = 293 K.Acknowledgements. A.N.M. acknowledges EOARD project 9IOE063 and related STCU partner project P751. R.H. acknowledges funding from the French National Research Agency through contract ANR-18-CE92-0052 “TOPELEC”. V.Y.R. acknowledges the support of COST Action CA17139.
[1] X. Chen, and C. Fang. Study of electrocaloric effect in barium titanate nanoparticle with core–shell model. Physica B: Condensed Matter 415, 14 (2013).
[2] B. Li, J. B. Wang, X. L. Zhong, F. Wang, Y. K. Zeng, and Y. C. Zhou. Giant electrocaloric effects in ferroelectric nanostructures with vortex domain structures. RSC Advances 3, 7928 (2013).
[3] Y. K. Zeng, B. Li, J. B. Wang, X. L. Zhong, W. Wang, F. Wang, and Y. C. Zhou. Influence of vortex domain switching on the electrocaloric property of a ferroelectric nanoparticle. RSC Advances 4, 30211 (2014).
[4] Z. Y. Chen, Y. X. Su, Z. D. Zhou, L. S. Lei, and C. P. Yang. The influence of the electrical boundary condition on domain structures and electrocaloric effect of PbTiO3 nanostructures. AIP Advances 6, 055207 (2016).
[5] F. Wang, L. F. Liu, B. Li, Y. Ou, L. Tian, and W. Wang. Inhomogeneous electric-field–induced negative/positive electrocaloric effects in ferroelectric nanoparticles. EPL (Europhysics Letters) 117, 57002 (2017).
[6] C. Ye, J. B. Wang, B. Li, X. L. Zhong, Giant electrocaloric effect in a wide temperature range in PbTiO3 nanoparticle with double-vortex domain structure. Sci. Rep. 8, 293 (2018).
[7] A. N. Morozovska, E. A. Eliseev, M. D. Glinchuk, H. V. Shevliakova, G. S. Svechnikov, M. V. Silibin, A. V. Sysa, A. D. Yaremkevich, N. V. Morozovsky, and V. V. Shvartsman. Analytical description of the size effect on pyroelectric and electrocaloric properties of ferroelectric nanoparticles. Phys. Rev. Materials 3, 104414 (2019).
[8] Yu. A. Barnakov, I. U. Idehenre, S. A. Basun, T. A. Tyson, and D. R. Evans. Uncovering the Mystery of Ferroelectricity in Zero Dimensional Nanoparticles. Royal Society of Chemistry, Nanoscale Adv. 1, 664 (2019).Speaker: Ms Hanna Shevliakova (Igor Sikorsky KPI) -
16:15
Coffee break 25m
-
16:40
Occupation-conservation transition in a quantum two-level system 20m
When we drive quantum two-level systems (or qubits) by periodical signals, we obtain repeatedly Landau-Zener-Stückelberg-Majorana (LZSM) transitions, which relates to the tunneling in qubits [1]. Recent interest for studying these repeated transitions is caused by the success in creation of the first quantum computing machines which are based on different types of connected driven qubits. We describe a transfer matrix (TM) approach [2], and its area of usability, for a single LZSM transition which started from a superpositional state. As the result, we obtain a formula for describing the final occupation probability with any superpositional initial state. We consider three types of a single transition, with: 1. Constructive interference, 2. Destructive interference, and 3. Occupation-conservation transition. The last one allows us to save the same occupation probability as before the transition. TM can also be used for describing repetitive transitions by using the result of the current transition as the initial condition for the next one. Previously in Ref. [3] the "transitionless transitions" in qubits were studied, there the author described only the case when initially a qubit was not in any superpositional state, but rather only in one of the basis states. In Fig. 1 we demonstrate constructive and destructive transition in comparison with numerical and analytic solution on the left side and occupation conservation case in the right panel, where also we demonstrated the range of possible final occupation probabilities.
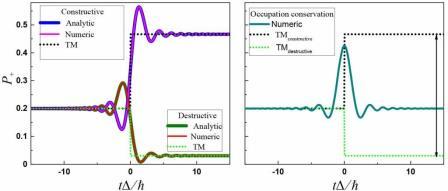
Fig. 1. (left) Constructive and destructive LZSM transitions, (right) Occupation-conservation transition, where the probability after passing the avoided-level crossing is exactly the same as it was initially. Both panels are plotted with the same initial conditions $P_{+i}=0.2$, the same parameters defining the transition probability, if starting from the ground state, $P_{LZSM}=0.081$, and with the initial phase difference $\phi_i$ being different in each case.Acknowledgment:
Research of O.V.I. and S.N.S. is sponsored by the Army Research Office and is accomplished under Grant Number W911NF-20-1-0261.[1] O.V. Ivakhnenko, S.N. Shevchenko, and F. Nori «Landau-Zener-Stückelberg-Majorana (LZSM) transitions for interferometry and quantum control», in preparation.
[2] B. Damski and W. H. Zurek, «Adiabatic-impulse approximation for avoided level crossings: from phase-transition dynamics to Landau-Zener evolutions and back again», Phys. Rev. A 73, 063405 (2006).
[3] M. V. Berry, «Transitionless quantum driving», J. Phys. A: Math. Theor. 42, 365303 (2009).Speaker: Mr Oleh Ivakhnenko (B. Verkin ILTPE of NASU) -
17:00
Resonant interferometry and spectroscopy of a double-quantum-dot system 20m
A double quantum dot system is a mesoscopic system with quantum properties in a semiconductor. It is one of the realizations of a two-qubit system. An external periodical driving of parameters of the system with avoided-level crossing causes nonadiabatic transitions and results in coherent interference fringes in the system’s occupation probabilities. For qubits with repelling energy levels, such interference, named after Landau-Zener-Stückelberg-Majorana, displays arc-shaped resonance lines. We demonstrate that the form of the resonances for systems without avoided-level crossings, such as the double quantum dot, change to harp-shaped one. We consider both stationary states and the dynamics, for which we solve the Lindblad equation. The form of the resonances can be used for system spectroscopy, which is important for potential applications of double quantum dots, such as multiple-electron transistors, solar cells, quantum computing.
Acknowledgment.
Research of A.I.R. and S.N.S. is sponsored by the Army Research Office and is accomplished under Grant Number W911NF-20-1-0261.Speaker: Mr Artem Ryzhov (ILTPE, Ukraine) -
17:20
Flat bands in quasi-one-dimensional Josephson junction arrays 20m
We study quasi-one-dimensional arrays of inductively coupled Josephson junctions with only self-inductance of a cell taken into account. A 2-row anisotropic Josephson junction ladder (JJL) has a flat band in the linear electromagnetic wave spectrum [1]. We derive the equations of motion for a 3-row anisotropic JJL and generalise them for a ladder with an arbitrary number of rows $ \kappa \geq 3 $. In the case of weak damping we obtain the spectrum of linear electromagnetic waves in these arrays. A $ \kappa $-row JJL has 3 bands in the spectrum, two of them are dispersive: the upper band consists of $ (\kappa-1) $ branches, the lower one of 2 branches, the band in the middle of the spectrum is dispersionless (flat) and is $ (\kappa - 2) $-fold degenerate. At zero external dc bias current the two lower branches become flat, resulting in $ \kappa $-fold degeneracy of the flat band.
The Authors acknowledge the support by the National Research Foundation of Ukraine grant ”Topological phases of matter and excitations in Dirac materials, Josephson junctions and magnets” (No. 2020.02.0051).
- A. E. Miroshnichenko, S. Flach, M.V. Fistul, Y. Zolotaryuk, J. B. Page. Breathers in Josephson junction ladders: Resonances and electromagnetic wave spectroscopy. $-$ PHYSICAL REVIEW E, VOLUME 64, 066601. $-$ 2001.
Speaker: Daryna Bukatova (Kyiv Academic University)
-
14:30
-
10:00
→
10:05
-
-
09:15
→
13:30
Astrophysics and Cosmology
-
09:15
Properties of star-forming galaxies: applications for cosmology 45m
The properties of nearby compact star-forming galaxies determined from recent studies are discussed. These galaxies are very similar to the galaxies in the early Universe and can be considered as building blocks for formation of giant galaxies. The important features of compact star-forming galaxies are low masses, low content of elements heavier than helium, and a very high star-forming activity. These properties make compact star-forming galaxies suitable for solving several cosmological problems. First of them is the search for and the detailed study of the galaxies with extremely low content of elements heavier than helium. Such galaxies are the best proxies of the earlist galaxies formed in the Universe. The second problem is related to the primordial nucleosynthesis, which is happened when the age of the Universe was only 2-3 minutes. Finally, the third discussed problem is the reionization of the Universe, which happened when its age was 200 - 1000 million years. For a reference, the age of the Universe now is 13.7 billion years.
Speaker: Prof. Yuriy Izotov (Bogolyubov Institute for Theoretical Physics of the National Academy of Sciences of Ukraine) -
10:00
Indirect dark matter search with future X-ray missions 30m
Dark matter (DM) remains one of the greatest problems to our understanding of cosmology.
In this talk I will briefly review several SM extensions which naturally provide dark matter candidates, including sterile neutrino, axion-like particles and dark photons. We will review existing constraints on the parameters of DM candidates and perspectives for indirect DM searches as well as discuss the improvement in the area which can be achieved with the next-generation X-ray missions such as Athena, eXTP and THESEUS.
Speaker: Dr Denys Malyshev (IAAT/Tubingen University) -
10:30
Annihilating Dark Matter Search with 12 Years of Fermi LAT Data in Nearby Galaxy Clusters 20m
Galaxy clusters are the largest virialised objects in the Universe, and as such, have a high dark matter (DM) concentration. This abundance of dark matter makes them promising targets for indirect DM searches. Here we report the details of a search, utilising almost 12 years of Fermi/LAT data, for gamma ray signatures from the pair annihilation of WIMP dark matter in the GeV energy band. From this, we present the constraints on the annihilation cross section for the bb, W+W- and γγ channels,derived from the non-detection of a characteristic signal from five nearby high galactic latitude galaxy clusters (Centaurus, Coma, Virgo, Perseus and Fornax). We discuss the potential of a boost to the signal due the presence of substructures in the DM halos of selected objects, as well as the impact of uncertainties in DM profiles on the presented results. We assert that the obtained limits are, within a small factor, comparable to the best available limits of those based on Fermi/LAT observations of dwarf spheroidal galaxies.
Speaker: Charles Thorpe-Morgan (Institut für Astronomie und Astrophysik - University of Tübingen) -
10:50
Neutron Star Cooling Within the Equation of State With Induced Surface Tension 20m
We study the thermal evolution of neutron stars described within the equation of state with induced surface tension (IST) that reproduces properties of normal nuclear matter, fulfills the proton flow constraint, provides a high-quality description of hadron multiplicities created during the nuclear-nuclear collision experiments, and it is equally compatible with the constraints from astrophysical observations and the GW170817 event. The model features strong direct Urca processes for the stars above $1.91~M_{\odot}$. The IST equation of state shows very good agreement with the available cooling data, even without introducing nuclear pairing. We also analysed the effect of the singlet proton/neutron and triplet neutron pairing on the cooling of neutron stars of different mass. We show that the description of the compact object in the center of the Cassiopeia A does not necessarily require an inclusion of neutron superfluidity and/or proton superconductivity. Our results indicate that data of Cassiopeia A can be adequately well reproduced by a $1.66~M_{\odot}$ star with an atmosphere of light elements. Moreover, the IST EoS reproduces each of the observational datasets for the surface temperature of Cassiopeia A either by a rapidly cooling $\sim$ $1.955~M_{\odot}$ star with paired and unpaired matter or by a $1.91 M_{\odot}$ star with the inclusion of neutron and proton pairings in the singlet channel.
Speaker: Mr Stefanos Tsiopelas (University of Coimbra) -
11:10
Revisiting constraints on warm dark matter from the UV luminosity functions 20m
The ultra-violet luminosity functions (UV LFs) of the galaxies allow constraining the dark matter particle properties. In the warm dark matter scenario, the formation of low-mass galaxies is suppressed, which may impact the UV LFs.
We have performed the Bayesian inference on warm and cold dark matter scenarios via UV LFs at z=6, 7, 8. We have found that there is no significant preference for the CDM over WDM by comparing the Bayesian evidences. Knowing the bayesian evidences allows us to build the combined bounds on the model parameters via different datasets. We have derived the robust combined bound on the warm dark matter particle mass $m_\text{x}\geq2.1$ keV with 95% confidence level.
Speaker: Anton Rudakovskyi (Bogolyubov Institute for Theoretical Physics) -
11:30
Coffee break 20m
-
11:50
Probing Solar Chromosphere Through Mg II h and k Wings at 280 nm 20m
The Chromospheric Layer Spectro-Polarimeter (CLASP2) was launched on April 11, 2019, from White Sands Missile Range on a sounding rocket and reached an altitude of 274 km above the sea level in the thermosphere. For five minutes in operation, it observed three different targets on the Sun: a quiet disc center, an active plage, and a quiet limb. One-dimensional slit spectra were taken in all four Stokes parameters in the vicinity of the resonance doublet of Mg II, the so-called h and k lines at 280 nm in the ultraviolet. A weak signal, although at the noise level, of linear polarization due to spatial symmetry breaking on atmospheric granulation was detected at the disc center target. The plage target showed strong signatures of the longitudinal Zeeman effect, as expected. The limb target revealed Q/I profile shapes due to the J-state interference in a two-term atom. This was the first observational confirmation of a theoretical effect predicted by Belluzzi and Trujillo Bueno (2012).
In order to interpret these observations, we developed two numerical modules for the radiative transfer code PORTA (Stepan and Trujillo Bueno, 2013). One module solves the polarized transfer equations neglecting effects due to magnetic fields, while the other includes the Faraday rotation via selected magneto-optical terms. Both modules account for the J-state interference as well as the partial redistribution of photons, scattered in the resonance doublet. As the general treatment of resonance scattering is too expensive, we approximated it by applying the atomic coherent scattering function in the observer's frame. This approximation kept the essential magnetic sensitivity in the wings and dramatically reduced computational costs. With both modules, we numerically solved the transfer problem in the wings of the Mg II doublet for a two-term model atom and using a model chromosphere from the so-called ``enhanced network simulations'' produced by the radiation-MHD code Bifrost (Carlsson et al. 2016). We generated both synthetic images as well as slit spectra in all four Stokes parameters for different positions on the solar disk, which we compared against observations.In this talk, I'll describe the observational experiment, the theoretical method, the complexity and computational demands of resonance scattering and how it can be approximated, which quantum effects define the observed shapes of the Stokes profiles, how sensitive to magnetic fields are the line wings, and why there are discrepancies between observed and calculated spectra.
Speaker: Dr Andrii V. Sukhorukov (Main Astronomical Observatory, NAS of Ukraine; Instituto de Astrofisica de Canarias, Tenerife, Spain) -
12:10
Radio to X-ray multiband sample for automated AGN search 20m
We present the sample of 18 846 spectroscopically confirmed AGNs found throughout radio to X-ray spectral bands. The sample consists of 10 344 AGNs selected among SDSS radio galaxies (Best, P. N.; Heckman, T. M., 2012 ), 5 536 galaxies with z < 0.09 from All-sky Optical AGN Catalogue (Zaw I., Chen Y.-P., Farrar G.R., 2019) and 3 345 AGNs from 3 catalogues in X-ray band - 1 632 from Swift BAT (Oh K. et. al, 2018), 1 444 from 3LAC (Ackermann M. et. al ,2015 ) and 269 AGN from XBS (Corral A. et. al, 2011). In order to complement selected objects with photometric information in 5 optical, 3 near-IR, and 4 mid-IR passbands, associations from PanSTARRS DR1 (Chambers K.C. et al., 2016) and AllWISE (Cutri R.M, et. al. 2013) catalogues were added. In this work, we discuss the criteria and strategy for the automated classification of AGN objects in modern photometric surveys.
Speaker: Kyrylo Soroka (Institute of Astronomy, V.N. Karazin Kharkiv National University,) -
12:30
Two-phase structure of ultralight dark matter with $\psi^6$ self-interaction. 20m
The ultralight dark matter (ULDM) model (also known as fuzzy dark matter or Bose-Einstein condensate dark matter) is one of alternatives to the cold dark matter (CDM) paradigm. It suggests that the dark matter particles are ultralight bosons with a tiny mass order of $10^{-22}$ eV, so that their de Broglie wavelength is of kiloparsec scale, that helps to resolve CDM tensions on the small scales. We consider ultralight scalar bosons condensate with $\psi^6$ self-interaction, which has a noticeable effect on the dark matter density distribution in highly dense regions, such as a central core of galactic dark matter halo or overlap of dark matter halo during the galaxies collision. At the same time, a contribution of tree-particles interaction is negligible in an outer part of the galactic dark matter halo and intergalactic medium. Thus all ULDM predictions on the large scales remain valid for the $\psi^6$ model, which, in turn, coincide with CDM predictions on these scales and are in agreement with observations. From the detailed analysis of thermodynamic characteristics of ULDM with $\psi^6$ self-interaction, we find the existence of two phases of dark matter separated by instability region in the (high density) core of dark matter halo.
Speaker: M. V. Khelashvili (Bogolubov Institute for Theoretical Physics) -
12:50
Triple Supermassive Black Hole evolution in NGC 6240 20m
One of the main possible ways to create the supermassive black hole (SMBH) is a so-called hierarchical merging scenario. At the final phase of interacting and colliding host galaxies, the central SMBHs are observed as SMBH binary (SMBHB) candidates at different separations from hundreds of pc to mpc. But only several triple SMBHs systems have been detected so far.
One of them is a well studied ULIRG galaxy NGC 6240 which was first spatially and spectroscopically resolved in X-rays by Chandra as SMBHB system. Later high-resolution data from MUSE instrument at the ESO VLT may resolve the third active galactic nuclei (AGN). Dynamical calculation of the central SMBH triple merging in a dense stellar environment allows us to retrace their evolution from kpc to mpc scales.
We present the set of direct N-body simulations with different particle numbers (N=67.5k, 135k, 240k, 540k) and five different randomizations of initial positions and velocities of particles.
We found the formation of hierarchical triple systems in approximately 80 per cent of systems, while other 20 per cent of systems fly apart. In large part of the formed hierarchical triple systems, we observe the oscillation of eccentricities and inclination between inner and outer orbits, which is the demonstration of Lidov-Kozai mechanism. This process can be one more mechanism to solve the merging BHs “last final parsec” problem.
Further detailed research of rare dual/multiple BHs in a dense stellar environment (based on observations data) can clarify the dynamical co-evolution of central BHs and their host-galaxies.Speaker: Margaryta Sobolenko (Main Astronomical Observatory NAS of Ukraine) -
13:10
High-energy and very high-energy gamma-ray emission from the magnetar SGR 1900+14 neighbourhood 20m
Magnetar wind nebulae (MWNe), created by new-born millisecond magnetars, and magnetar giant flares are PeVatron candidates and even potential sources of ultra high energy (E>1018 eV) cosmic rays (UHECRs). Nonthermal high-energy (HE, E>100 MeV) and very high-energy (VHE, E>100 GeV) γ-ray emission from magnetars neighbourhoods should be a promising signature of acceleration processes. We investigate a possibility of explaining HE and VHE γ-ray emission from the vicinity of the magnetar SGR 1900+14 by cosmic rays accelerated in a Supernova remnant of a magnetar-related Supernova and/or in a MWN. Simulation of the observed HE (the extended Fermi-LAT source 4FGL J1908.6+0915e) and VHE (the extended H.E.S.S. source candidate HOTS J1907+091 and the point-like HAWC TeV source 3HWC J1907+085) γ-ray emission, spatially coincident with the magnetar SGR 1900+14, was carried out in the framework of hadronic (pp collisions with a subsequent pion decay) and leptonic (inverse Compton scattering of low energy background photons by ultrarelativistic electrons) models. We show that under reasonable assumptions about parameters of the circumstellar medium the observed γ-ray emission of Fermi-LAT 4FGL J1908.6+0915e, H.E.S.S. HOTSJ1907+091 and 3HWC J1907+085 sources may be explained or at least considerably contributed by a (still undetected) magnetar-connected Hypernova remnant and/or a MWN created by new-born millisecond magnetar with a large reserve of rotational energy Erot∼1052 erg.
Speaker: Mr Vadym Voitsekhovskyi (Astronomical Observatory of Taras Shevchenko National University of Kyiv)
-
09:15
-
13:30
→
14:30
Lunch 1h
-
14:30
→
15:50
Physics of Nuclei and Elementary Particles
-
14:30
Lambda spin polarization in QGP. 20m
Measurements made recently by the STAR collaboration show that the Lambda hyperons produced in relativistic heavy-ion collisions are subject to global spin polarization with respect to an axis coincident with the axis of rotation of the produced matter. Recently formulated formalism of relativistic hydrodynamics with spin, which is a generalization of the standard hydrodynamics, is a natural tool for describing the evolution of such systems. This approach is based on the conservation laws and the form of the energy-momentum tensor and spin tensor postulated by de Groot, van Leeuwen, and van Weert (GLW). Using Bjorken symmetry we show how this formalism may be used to determine observables describing the polarization of particles measured in the experiment.
Speaker: Rajeev Singh (Institute of Nuclear Physics Polish Academy of Sciences) -
14:50
Dualities in QCD phase diagram 20m
The talk is devoted to QCD phase diagram studies, including the region of large baryon density that will be probed at NICA.
Recently it has been shown that in the large-Nc limit (Nc is the number of colors of quarks) there exist duality correspondences (symmetries) in the phase portrait, which are the symmetries of the thermodynamic potential and the phase structure itself. The first one is a duality between the chiral symmetry breaking and the charged pion condensation phenomena. And there are two other dualities that hold only for chiral symmetry breaking and charged pion condensation phenomena separately. For example, we have shown that charged pion condensation does not feel the difference between chiral and isospin imbalances of the medium. They were shown to exist in the matter with chiral imbalance that can be produced in compact stars or heavy ion collisions. One of the key conclusions of these studies is the fact that chiral imbalance generates charged pion condensation in dense baryonic/quark matter. It was shown that our results in particular cases are consistent with the simulation of lattice QCD, which is possible in these cases.
Duality was used to show that there takes place catalysis of chiral symmetry breaking by chiral imbalance.
It was also shown that chiral imbalance generates the phenomenon of charged pion condensation in dense baryonic/quark matter even in the case of charge neutral matter, which is interesting in the context of the astrophysics of neutron stars.
It is known that chiral imbalance can occur in high energy experiments of the collision of heavy ions, due to temperature and sphaleron transitions. Our studies show that different types of chiral imbalance can occur in the cores of neutron stars or in heavy ion experiments, where large baryon densities can be reached, due to another phenomena - the so-called chiral separation and chiral vortical effects.
Duality was shown to exist even in case of inhomogeneous condensates. This example shows that the duality is not just entertaining mathematical property but an instrument with very high predictivity power.
The unified picture and full phase diagram of isospin imbalanced dense quark matter have been assembled. Acting on this diagram by a dual transformation, we obtained, in the framework of an approach with spatially inhomogeneous condensates and without any calculations, a full phase diagram of chirally asymmetric dense medium.
Continuing our studies of dualities, we noted that there are dualities in 2-color QCD that are connected with adiitional symmetry of QCD with two colors namely Pauli-Gursey symmetry.
It has been also shown that found duality is a more fundamental and can be shown at the level of Lagrangian. It has been shown that duality is a property of real QCD. It is not bounded by large Nc approximation and exists in the cases of 2 and 3 and infinite number of colours.References:
Phys.Rev. D95 (2017) no.10, 105010
Phys.Rev. D97 (2018) no.5, 054036
Phys.Rev. D98 (2018) no.5, 054030
Eur.Phys.J. C79 (2019) no.2, 151
JHEP 1906 (2019) 006
Phys. Rev. D 100, 034009 (2019)
JHEP 06 (2020) 148
Eur.Phys.J.C 80 (2020) 10, 995Speaker: Dr Roman Zhokhov (IZMIRAN, Troitsk, Moscow; IHEP, Protvino) -
15:10
Dark Matter Polarization Operator in the Generalized Yukawa Model 20m
The dark matter particle candidates are searched on various modern colliders, but nothing has been found, yet. The possible reason for this is considered in this work. In the on-resonance search method of the new particle, the latter is identified with the resonant peak in the cross-section of some scattering process. The resonance position coincides with the mass of the particle, and its width is defined as peak width on the half of its height. It is assumed in the experimental data treatment that the new resonance is narrow, namely its width is up to $3\%$ of its mass. If it is wider, such state could be missed in the data as a noise. We consider different scenarios in which dark matter candidate acquires bigger width, and identify the new particle parameters at which it happens.
We conduct our research in the framework of the generalized Yukawa model, where dark matter is presented as a scalar field $\chi$ and a Dirac fermionic field $\Psi$. The model also contains the sector of visible matter particles, which consists of scalar field $\phi$ and Dirac fermionic fields $\psi_1$ and $\psi_2$. The lagrangian of the model reads:
$ \mathcal{L} = \frac{1}{2}\left[\left(\partial_{\mu}\phi\right)^2 - \mu^2\phi^2 + \left(\partial_{\mu}\chi\right)^2 - \Lambda^2\chi^2\right] - \lambda\phi^4 - \rho\phi^2\chi^2 - \xi\chi^4 + $
$ + \sum\limits_{a=1;2}\bar{\psi}_a\left(i\gamma^{\mu}\partial_{\mu} - m_a - g_{\phi}\phi - g_{\chi}\chi\right)\psi_a + \bar{\Psi}\left(i\gamma^{\mu}\partial_{\mu} - M - G_{\chi}\chi\right)\Psi. $Width of the $\chi$ particle is defined generally by the imaginary part of its polarization operator $\Pi_{\chi\chi}(p^2)$ taken at the point $p^2 = \Lambda^2$. Here $p^2$ is the squared momentum transferred through the virtual bosonic state. $\Pi_{\chi\chi}(p^2)$ is found analytically. Hence, the width $\rho$ of the $\chi$ resonance, as a fraction of mass $\Lambda$, reads:
$$ \rho = \frac{\Im\Pi_{\chi\chi}(\Lambda^2)}{\Lambda^2} = \frac{g_{\chi}^2}{8\pi}\left[\left(1 - \frac{4m_1^2}{\Lambda^2}\right)^{\frac{3}{2}} + \left(1 - \frac{4m_2^2}{\Lambda^2}\right)^{\frac{3}{2}}\right] + \frac{G_{\chi}^2}{\Lambda^2}\left(1 - \frac{4M^2}{\Lambda^2}\right)^{\frac{3}{2}}. $$ The lagrangian also introduces the mixing of scalar fields, which occurs on the one-loop level. That is, two-point Green function $\left<0\left|T\phi(x_1)\chi(x_2)\right|0\right>$ becomes non-zero due to the loop correction from the $\psi_1$ and $\psi_2$, which connects $\phi$ and $\chi$ lines on the corresponding diagram. The magnitude of such mixing is defined by the corresponding mixing angle $\theta_{mix}$. We define this angle from the diagonalization of the bosonic mass matrix, which is given by the effective potential of the scalar fields. Hence, $\theta_{mix}$ reads: $$ \tan{2\theta_{mix}} = 2g_{\phi}g_{\chi}F\left[\frac{4\pi^2}{3}\left(\Lambda^2 - \mu^2\right) + \left(g_{\phi}^2 - g_{\chi}^2\right)F - G_{\chi}^2M^2\ln\frac{M^2}{\kappa^2}\right]^{-1}, $$ $$ F = m_1^2\ln\frac{m_1^2}{\kappa^2} + m_2^2\ln\frac{m_2^2}{\kappa^2}, $$ where $\kappa$ is an arbitrary renormalization parameter. From the explicit analytical expression, we find areas of the model parameters space where $\rho\cdot 100\% > 3\%$. We find that the limit of $3\%$ can be exceeded in many cases. In the framework of our model, the conditions for that are the following. There should be $\Lambda > \mu$, so DM particle is heavier than the visible one. Additionally, interactions in the visible sector should be weaker than that of between the dark and visible particle or between the particles in the dark sector only. That is, if either $g_{\chi} \gg g_{\phi}$ or $G_{\chi} \gg g_{\phi}$. Finally, there exists an upper bound for the mixing angle -- in our model, it should be $|\theta_{mix}|\leq 10^{-5}$. We find that until mixing between visible and dark bosons is small and two resonances are located far enough one from another, the parameters of visible particle resonance are independent of the characteristics of the dark sector. In this case dark resonance is both wide and does not interfere with the resonance of visible $\phi$. The presence of the upper limit on $\theta_{mix}$ is qualitatively important.
The self-interaction of the bosonic particles does not affect their widths, being canceled in the renormalization procedure.
The considered Yukawa model gave a possibility for analyzing the role of the masses and couplings of particles. Other aspects of the problem such as group symmetry of the extended model and, hence, the content of the states remain behind it. However, we have obtained the set of conditions which have to be taken into account when searches for the DM particles are carried out. In general, to avoid the problem of wide resonance states we have to apply additionally non-resonant methods to detect these new states of matter.
Speaker: Mykyta Dmytriiev -
15:30
S-Matrix unitarity and Pomeron shadowing corrections 20m
Regge theory is the only valid framework to describe soft scattering processes where the perturbative QCD is not applicable. In Regge theory, the particle diffraction is treated as an exchange of some 'object' called Pomeron (which in some way generalizes a particle — in particular, it is described by variable complex angular momentum which generalizes a spin). That approach was found surprisingly useful to phenomenologically calculating cross sections.
In 1960s, it was shown that multi-Pomeron shower production reactions $pp \rightarrow p + X_1 + X_2 + ... + p$, where showers $(X_i)$ are separated by large rapidity gaps, are breaking the S-matrix unitarity because corresponding cross-sections $\sigma_{tot}$ grow with the rapidity ($\xi$) faster than allowed by unitarity (the upper bound is $\sigma_{tot} \leq \xi^2$). This issue is known as Finkelstein-Kajantie problem. In 1974, a possible solution was proposed [1] in multi-channel Eikonal model. It considered the gap survival probability $S^2$ — the probability to observe the pure process where the gap is not populated by secondaries produced in the additional inelastic interaction. In the impact parameter representation the probability is given by $S^{2}(b) = |e^{-\Omega(b)}|$, where $b$ is the impact parameter and $\Omega$ is the proton opacity. In the black disc limit $Re(\Omega) \rightarrow \infty$, so $S^2(b) \rightarrow 0$. So the additional rescatterings should close the rapidity gaps. The work [2] shows that decreasing of the survival probability should overcompensate the original cross-sesction growth so, as a result, the cross-sections should also vanish with energy: $\frac{d\sigma}{d\xi_1} \sim e^{-{\Delta}\xi_1} \rightarrow 0$, where $\xi_1$ is the shower width on the rapidity scale. If the result is correct then the unitarity is restored. Over the past decades, it has been considered a cure for the FK problem [3].
The work [4] had discovered that such an approach still fails to unitarize the Pomeron contribution to the single diffraction dissociation amplitude due to an error in the calculations. The suspicion had arised: is the cure really effective in terms of all the processes it is purposed for? Recent TOTEM soft scattering data renewed the interest to these questions.
In the work [5] we investigate the survival probability method for all the diffractive processes. The main processes are next. The first is single diffraction dissociation where one of the two incoming protons transforms into a shower: $pp \rightarrow X + p$. The second is double diffraction dissocastion where both protons transforms: $pp \rightarrow X_1 + X_2$. The third is central production: $pp \rightarrow p + X + p$. Integrated cross-sections of all these processes behave similar to each other, so only the simplest, the single dissociation, will be considered in this talk. Its cross-section contains a multiplier $e^{\Delta(\xi_1 + 2\xi_2 - a\xi)}$, where $a \rightarrow 2\frac{\xi}{\xi + \xi_1}$ as $\xi \rightarrow \infty.$ Here $\xi_2$ is the rapidity gap between the produced shower and the initial proton; $\xi_1 + \xi_2 = \xi$ — the overall rapidity difference between interacting protons. While investigating the high energy asymptotics ($\xi \rightarrow \infty$), the authors of [2] considered $a$ as $2$ and $e^{\Delta(\xi_1 + 2\xi_2 - a\xi)}$ simply became $e^{-\Delta{\xi_1}}$. However, if the calculations are done in an explicit way, one can see that $a = 2(1 -\frac{\xi_1}{\xi} + O(\frac{\xi^2_1}{\xi^2}))$ and so $e^{\Delta(\xi_1 + 2\xi_2 - a\xi)} = e^{\Delta(\xi_1 + 2\xi_2 - 2\xi (1 -\frac{\xi_1}{\xi}))}$ = $e^{+\Delta{\xi_1}}$, thus the fast cross-section growth is in fact maintained.
Thereby the existing survival probability methods are unable to keep the cross-section growth within the unitarity bound. We develop a different approach based on the Pomeron and triple-Pomeron vertex renormalization via Schwinger-Dyson equations. We take the Pomeron in it's maximal form providing the maximal strong interactions strength allowed by unitarity. The triple-Pomeron vertex is chosen to contain zeroes at some transferred momenta and complex angular momenta. The parameters of developing model can be chosen in such a way that the unitarity bounds are not violated.[1] J. L. Cardy. General Features of the Reggeon Calculus with $\alpha > 1$. Nucl. Phys. B, 75 (1974)
[2] E. Gotsman, E.M. Levin, U. Maor. Diffractive Dissociation and Eikonalization in High Energy $pp$ and $p\bar{p}$ Collisions, Phys. Rev. D, 49 (1994)
[3] V.A. Khoze, A.D. Martin, M.G. Ryskin. Black disc, maximal Odderon and unitarity. Phys.Lett. B, 780 (2018)
[4] E. Martynov, B. Struminsky. Unitarized model of hadronic diffractive dissociation. Phys.Rev. D, 53 (1996)
[5] E. Martynov, G. Tersimonov. Multigap diffraction cross sections: Problems in eikonal methods for the Pomeron unitarization. Phys. Rev. D, 101 (2020)Speaker: Georgy Tersimonov (Bogolyubov Institute for Theoretical Physics)
-
14:30
-
15:50
→
16:30
Mathematical Physics
-
15:50
Detecting geometric measure of entanglement of graph states on quantum computer 20m
Graph states generated by operator of evolution with Ising Hamiltonian are studied. The geometric measure of entanglement of the states is quantified analytically. For this purpose relation of the geometric measure of entanglement with the mean value of the spin is used (the relation was obtained in [1]). Also, quantum protocol for preparing graph states of spin system with Ising interaction is constructed. The geometric measure of entanglement of the states is detecting on the IBM's quantum computers.
We obtained that entanglement of spin with other spins in the graph state depends on the graph properties, namely it depends on the degree of vertex that corresponds to the spin.[1] A. M. Frydryszak, M. I. Samar, V. M. Tkachuk, Eur. Phys. J. D 71, 233 (2017).
Speaker: Khrystyna Gnatenko (Ivan Franko National University of Lviv, Department for Theoretical Physics) -
16:10
Effective free-fermionic form factors on a lattice and XY quantum chain 20m
We introduce the effective form factors for one-dimensional lattice fermions with arbitrary phase shifts. We study tau functions defined as series of these form factors. On the one hand we perform the exact summation and present tau functions as Fredholm determinants in the thermodynamic limit. On the other hand simple expressions of form factors allow us to present the corresponding series as integrals of elementary functions. Using this approach we re-derive the asymptotics of static correlation functions of the XY quantum chain at finite temperature.
Speaker: Yurii Zhuravlov (Bogolyubov Institute for Theoretical Physics of the National Academy of Sciences of Ukraine)
-
15:50
-
16:30
→
16:45
Coffee break 15m
-
16:45
→
18:30
Statistical Theory of Many-body Systems
-
16:45
Dynamics of micro-organisms controlled by liquid crystals 45m
Microscale active systems such as swarms of swimming bacteria and cell tissues demonstrate fascinating dynamics that can potentially be used in applications ranging from micro-robotics to regenerative medicine. Control of this dynamics in isotropic media such as water is difficult. We describe an approach in which instead of an isotropic medium, the dynamics of micro-organisms is guided by a liquid crystal. An example with a droplet of an active bacterial suspension shows an immediate benefit of such a replacement: when placed in an isotropic fluid, the droplet experiences random Brownian motion, but once the medium becomes a nematic liquid crystal, the droplet acquires an ability to swim unidirectionally along a prescribed trajectory [1]. Other examples of liquid crystal control over the dynamics of microscopic objects include dynamic swarms of swimming bacteria [2-4] and living tissues formed by human dermal fibroblasts [5]. Director gradients and topological defects impact the biological microstructures most strongly, causing spatial variation of bacterial concentration and cell phenotype and shaping irreversible active flows. The physical mechanisms are shaped by the nontrivial effect of the orientastional order of a liquid crystal on the interactions of dynamic active units. The control of active matter by patterned liquid crystals might result in new approaches to harness the energy of collective motion for micro-robotic, biomechanical, biomedical, and sensing applications.
The work is supported by NSF DMR-1905053, CMMI-1663394, and DOE DE-SC0019105 grants.
[1] M. Rajabi, B. Hend, T. Turiv, and O. D. Lavrentovich, Directional self-locomotion of active droplets enabled by nematic environment, Nature Physics, https://doi.org/10.1038/s41567-41020-01055-41565 (2020).
[2] C. Peng, T. Turiv, Y. Guo, Q.-H. Wei, and O. D. Lavrentovich, Command of active matter by topological defects and patterns, Science 354, 882-885 (2016).
[3] T. Turiv, R. Koizumi, K. Thijssen, M. M. Genkin, H. Yu, C. Peng, Q.-H. Wei, J. M. Yeomans, I. A. Aranson, A. Doostmohammadi, and O. D. Lavrentovich, Polar jets of swimming bacteria condensed by a patterned liquid crystal, Nature Physics 16, 481–487 (2020).
[4] R. Koizumi, T. Turiv, M. M. Genkin, R. J. Lastowski, H. Yu, I. Chaganava, Q.-H. Wei, I. S. Aranson, and O. D. Lavrentovich, Control of bacterial swirls by spiral nematic vortices: Transition from individual to collective motion and contraction, expansion, and stable circulation of bacterial swirls, Physical Review Research 2, 033060 (2020).
[5] T. Turiv, J. Krieger, G. Babakhanova, H. Yu, S. V. Shiyanovskii, Q. Wei, -H., M.-H. Kim, and O. D. Lavrentovich, Topology control of human fibroblast cells monolayer by liquid crystal elastomer, Science Advances 6, eaaz6485 (2020).Speaker: Prof. Oleg Lavrentovich (Advanced Materials and Liquid Crystal Institute, Department of Physics and Materials Science Graduate Program, Kent State University) -
17:30
Compressibility and compactivity of bi-dispersive many-particle conglomerations (liquid and granular mixtures) 20m
We propose to use the apparatus of Kirkwood-Buff theory [1] in combination with Carnahan-Starling model [2] and Mansoori [3] equations of state together with the relevant phenomenological information, which obtained from the direct observations, to describe compressibility and compactivity of bi-dispersive many-particle conglomerations (liquid [4] and granular mixtures [5]). By use of above mentioned approach we found the possibility to describe substantiate empirical data in the full range of values of the volume (or molar) fraction. A good coincidence between theoretical and relevant experimental data has been outlined.
[1]. Kirkwood J.G., Buff F.P. The statistical mechanical theory of solutions. I. J. Chem. Phys. 19(6), 774-777 (1951) https://doi.org/10.1063/1.1748352
[2]. Carnahan N.F., Starling K.E. Equation of state for nonattracting rigid spheres. I. J. Chem. Phys. 51(2), 635-636. (1969) https://doi.org/10.1063/1.1672048
[3]. Mansoori G.A., Carnahan N.F., Starling K.E., Leland jr. T.W. Equilibrium Thermodynamic Properties of the Mixture of Hard Spheres. J. Chem. Phys. 54(4), 1523-1525 (1971) https://doi.org/10.1063/1.1675048
[4]. Aliotta F., Gapiński J., Pochylski M., Ponterio R.C., Saija F., Salvato G. Excess compressibility in binary liquid mixtures. J. Phys. Chem. 126(22), 224508 (2007) https://doi.org/10.1063/1.2745292
[5]. Pilliteri S., Lumay G., Opsomer E., Vandewalle N. From jamming to fast compaction dynamics in granular binary mixtures. Sci. Rep. 9(1), 7281 (2019) https://doi.org/10.1038/s41598-019-43519-6Speaker: Mr Andrii Spivak (Odesa State Environmental University) -
17:50
On relaxation processes in plasma 20m
The plasma is considered in a generalized Lorentz model which contrary to standard one assumes that ions form an equilibrium system. Following to Lorentz it is neglected by electron-electron and ion-ion interactions. Relaxation of the electron energy and momentum densities is investigated in spatially uniform states of completely ionized plasma in the presence of small constant and spatially homogeneous external electric field. The kinetic equation is given by the formula:
$\left[{\partial _t}{{\rm{f}}_p}(t) = - {F_n}\frac{{\partial {{\rm{f}}_p}(t)}}{{\partial {p_n}}} + {I_p}({{\rm{f}}_{p'}}(t))\right]$, (${F_n} = - e{E_n}$, $\int {{d^3}p{{\rm{f}}_p}(t) = n} $), (1)
where ${E_n}$ is external electric field, $ - e$ is charge of an electron, $n$ is electron density. Perturbation theory is created in terms of spectral theory of operator of collision integral ${\bf{K}}$, which could be defined as ${\bf{K}}{a_p} = - w_p^{ - 1}{I_p}({w_{p'}}{a_{p'}})$ (${w_p}$ is Maxwell distribution; ${I_p}({w_{p'}}) = 0$). Linear operator ${\bf{K}}$ is a symmetric and positively defined one. Complete orthonormal system of its own functions ${g_{ip}}$ could be used to find solutions of kinetic equation (1) as series by mods:
${{\rm{f}}_p} = {w_p}(1 + {g_p})$, ${g_p} = \sum\limits_i {{c_i}{g_{ip}}} $. (2)
We use irreducible polynomials as our own functions. The scalar ${A_p}$ and vector ${B_p}{p_l}$ eigenfunctions and corresponding eigenvalues ${\lambda _{\,T}}$, ${\lambda _u}$ play a decisive role among its own functions
${\bf{K}}{A_p} = {\lambda _{\,T}}{A_p}$, ${\bf{K}}{B_p}{p_l} = {\lambda _u}{B_p}{p_l}$ ($\langle {A_p}{\varepsilon _p}\rangle \equiv 3n/2$, $\langle {B_p}{\varepsilon _p}\rangle \equiv 3n/2$). (3)
It is convenient to investigate the relaxation processes in the system in terms of average electron energy $\varepsilon $ and momentum ${\pi _l}$ densities. It is established that their evolution is exact described at all times by scalar and vector modes
$\left[\varepsilon = {\varepsilon _0} + {c_T}3n/2\right]$, $\left[{\pi _l} = mn{c_{{u_l}}}\right]$, (${\varepsilon _0} \equiv 3nT/2$), (4)
where ${c_T}$, ${c_{{u_l}}}$ – coefficients in series (2) with its eigenfunctions ${A_p}$, ${B_p}{p_l}$ ($m$ – electron mass, ${T_0}$ – ion system temperature). It is proved that quantities $\varepsilon $ і ${\pi _l}$ at all times and for an arbitrary external electric field ${E_n}$ satisfy the equation:
$\left[{\partial _t}{\pi _l} = n{F_l} - {\lambda _u}{\pi _l}\right]$, $\left[{\partial _t}\varepsilon = \frac{1}{m}{\pi _l}{F_l} - {\lambda _{\,T}}(\varepsilon - {\varepsilon _0})\right]$. (5)
The results (4), (5) were found by using irreducible tensors as eigenfunctions of the operator ${\bf{K}}$. Formulas (5) show that eigenvalues ${\lambda _{\,T}}$, ${\lambda _u}$ describe relaxation process in the absence of external electric field
$\varepsilon \to \varepsilon_0$, when ${t\gg\tau_{T}}$ and $\pi _l \to 0$, when ${t\gg\tau_{u}}$, (${\tau _T} \equiv 1/{\lambda _{\,T}}$, ${\tau _u} \equiv 1/{\lambda _u}$). (6)
In terms of temperature $T$ and velocity ${u_l}$ of electron system
$\varepsilon \equiv 3nT/2 + mn{u^2}/2$, ${\pi _l} \equiv mn{u_l}$ (7)
equations (5) take the form
${\partial _t}T = - {\lambda _T}(T - {T_0}) + (2{\lambda _u} - {\lambda _T})m{u^2}/3$, ${\partial _t}{u_n} = - {\lambda _u}{u_n} + \frac{1}{m}{F_n}$ (8)
These equations are exact and valid at all times and arbitrary electric field. The first one does not contains the electric field. At equilibrium equation (8) gives
${u_l}(t)\mathop = \limits_{t > > {\tau _T},{\tau _u}} u_l^{eq}$, $u_l^{eq} = - \nu {E_l}$, $\nu \equiv \frac{e}{{m{\lambda _u}}}$; $j_l^{eq} = \sigma {E_l}$, $\sigma \equiv \frac{{{e^2}n}}{{{\lambda _u}}}$;
$T(t)\mathop = \limits_{t > > {\tau _T},{\tau _u}}{T^{eq}}$, ${T^{eq}} = {T_0} + \Delta T$, $\Delta T \equiv \frac{{{e^2}(2{\lambda _u} - {\lambda _T})}}{{3m{\lambda _T}\lambda _u^2}}{E^2}$ (9)
The expression for the mobility of electrons $\nu$ and the plasma conductivity $\sigma $ in (9) are exact. The last formula accurately describes the effect of temperature differences between the electron and ion components of the plasma in equilibrium in the presence of an electric field. This effect was previously discussed in [2] as an approximate result and without accuracy control.[1] Sokolovsky А.I., Sokolovsky S.A., Нrinishyn O.A. On relaxation processes in a completely ionized plasma. East European Journal of Physics. Vol. 3 (2020). P. 19-30; doi.org / 10.26565/2312-4334-2020-3-03.
[2] Smirnov В.М. Kinetika elektronov v gazakh i kondensirovannykh sistemakh. UFN Vol. 172 (12) (2002). – P. 1411-1445 (in Russian).Speaker: Oleh Hrinishin
-
16:45
-
09:15
→
13:30
-
-
09:00
→
12:00
Condensed Matter Physics
-
09:00
Probing and manipulating valley coherence of dark excitons in WSe$_2$ monolayer 40m
Monolayers of semiconducting transition metal dichalcogenides are two-dimensional direct-gap systems that host tightly-bound excitons with an internal degree of freedom corresponding to the valley of the constituting carriers. Strong spin-orbit interaction and the resulting ordering of the spin-split subbands in the valence and conduction bands makes the lowest-lying excitons in WX$_2$ (X being S or Se) spin-forbidden and optically dark. This results in their long lifetime, making them potentially interesting for valleytronics. With polarization-resolved photoluminescence experiments performed on a WSe$_2$ monolayer encapsulated in a hexagonal boron nitride, we demonstrate how the intrinsic exchange interaction in combination with the applied in-plane and perpendicular magnetic fields enables one to probe and manipulate the valley degree of freedom of the dark excitons.
Speaker: Dr Artur Slobodeniuk (Charles University) -
09:40
Surface waves on resonant anisotropic metasurfaces 20m
This work presents the results of theoretical and experimental studies and control of the properties (dispersion, polarization, phase and spatial distribution, directivity, optical spin) of surface electromagnetic waves localized on anisotropic resonant metasurfaces in the optical, near-IR and microwave ranges.
Speaker: Dr Oleh Yermakov (Department of Сomputer Physics, V. N. Karazin Kharkiv National University) -
10:00
Collective oscillations of plasma and order parameter in graphene counterflow superconductors. 20m
It is known [1] that in systems with Cooper pairing a specific collective excitations can exist, such as: the Anderson–Bogoliubov mode (oscillations of the phase of the order parameter), the Schmid mode (oscillations of the modulus of the order parameter), and the Carlson–Goldman mode (coupled oscillations of the phase of the order parameter and the scalar potential). These modes can exist under certain conditions. A genuine Anderson–Bogoliubov mode can appear in neutral superfluids, and the Carlson–Goldman mode exists in a very narrow temperature range near $T_c$.
We consider [4] a possibility of these modes existence in a double layer graphene system with electron-hole pairing. Such a system consists of two parallel graphene layers, which are spatially separated. If one layer has an electron conductivity and the other layer has a hole conductivity, then electrons and holes from the opposite layers can form pairs, which are similar to the Cooper pairs. This system is an example of a so-called counterflow superconductor [2,3].
The influence of electron-hole pairing in the double layer graphene system on collective plasma excitations is investigated under accounting for the order parameter fluctuations. It is established that out-of-phase oscillations of the order parameters of two spin subsystems are uncoupled from electromagnetic field oscillations. The spectrum of these oscillations splits into two branches: a low-energy (weakly damped, $\hbar\omega < 2\Delta$) and high-energy (strongly damped, $\hbar\omega > 2\Delta$) ones. Here $2\Delta$ is the gap in the electron spectrum caused by the pairing. The low-energy branch can be considered as an analog of Anderson–Bogoliubov mode and the high-energy—as an analog of Schmid mode. At small wave vectors $q$ the Anderson–Bogoliubov mode has an acoustic dispersion $\omega \approx q v_{F} / \sqrt{2}$ ($v_{F}$ is the Fermi velocity), and its frequency saturates at $\hbar \omega = 2\Delta$ at large $q$. The Schmid mode exists only at small $q$.
It is shown that in-phase oscillations of the order parameters of two spin subsystems are hybridized with out-of-phase oscillations of scalar potentials in layers. The spectrum of these oscillations also splits into two branches: a low-energy (weakly damped, $\hbar\omega < 2\Delta$) and high-energy (strongly damped, $\hbar\omega > 2\Delta$). The low-energy mode can be interpreted as Carlson–Goldman mode and the high-energy—as a strongly damped acoustic plasmon mode. The Carlson–Goldman mode exists at all temperatures below the critical one, in contrast with conventional superconductors in which this mode appears only near the critical temperature. Similarly to the Anderson–Bogoliubov mode, the Carlson–Goldman mode demonstrates an acoustic dispersion at small $q$ and its frequency saturates at $\hbar \omega = 2\Delta$ at large $q$.
It is established [4,5] the existence of two symmetric (optical) plasmon modes in counterflow superconductors, which correspond to in-phase oscillations of the scalar potentials in the layers. These modes are uncoupled from order parameter oscillations.[1] I. O. Kulik, Ora Entin-Wohlman, and R. Orbach, J. Low Temp. Phys. 43, 591 (1981).
[2] S. I. Shevchenko, Sov. J. Low Temp. Phys. 2, 251 (1976).
[3] D. V. Fil and S. I. Shevchenko, LTP 44, 867 (2018).
[4] K. V. Germash and D. V. Fil, Phys. Rev. B 99, 125412 (2019).
[5] K. V. Germash and D. V. Fil, Phys. Rev. B 93, 205436 (2016).Speaker: Mr Kostiantyn Hermash (Institute for Single Crystals of NAS of Ukraine) -
10:20
Formation of regular domain structures with small period in ferroelectrics during phase transitions 20m
Regular domain structures (RDS) with submicron period are widely used in nonlinear optics, non-volatile memory and laser investigations, which causes a significant interest in research to create the new methods for its fabrication. Classical methods of the RDSs formation do not allow us to achieve the required high precision necessary for modern devices. Within the framework of the Landau – Ginzburg phenomenological theory an innovative method for fabrication RDS with micron and submicron period was proposed.
Using the lithium tantalate crystal as an example, the kinetics of ordering of high non-equilibrium domain structure near Curie point under the influence of external high-frequency electric field was investigated. It was shown that the quenching depth of the sample influences on the nature of the evolution of the system, but not on its final result. Independently of the quenching depth, the system evolves to a polydomain (regular) structure, which remains stable even when the external electric field is turned off.
There was shown that the effect of the external high-frequency electric field on the relaxing domain structure has a threshold character depending on the frequency and the amplitude of the electric field. Critical values of these parameters for ferroelectrics that undergo the second order phase transition can be observed from the model. For lithium tantalate crystal the critical frequency is $f_{cr}$ = 4.8∙1010 Hz and the critical amplitude is $E_{cr}$ = 1.26∙106 V/m (Fig. 1). The RDS formation takes place in cases, when $f > f_{cr}$ or $E < E_{cr}$. The second variant is preferable because of the minimal risk of the crystal destruction. The numerical analysis showed the thermodynamic stability of the formed RDS even after turning off the external electric field. It was shown, that near Curie point $(T_C – T_1 ≤ 3K)$ the critical value of the amplitude substantially depends on the quenching depth, which may be related to the size of the initial inhomogeneities. With deep quenching $(T_C – T_1 > 3K)$ the critical value of the amplitude is determined only by the frequency of the external electric field (Table 1).
Fig 1. Phase trajectories of the system for the parameters $r_c(0)=2$, $\overline{\pi}_0=0$, $D_0=0.001$, $f=10^{10}$ Hz, $\alpha=0.03$. Curves 1-4 correspond to the amplitudes of electric field $|\varepsilon_m|$: {0.01; 0.031; 0.0315; 0.05} respectively (in dimensionless units)

Table 1. Critical values of the amplitude of the external electric field $E_{cr}(10^5 V/m)$ depending on the frequency $\Omega$ and quenching temperature $T_1$There was shown that the evolution of domains can occurs with the formation of short-lived quasistationary asymmetric polydomain phases, which can exist up to several minutes (Fig. 1). The developed model is not only applied, but also fundamental. The relaxation process is accompanied by a gradual enlargement of the domain structure, which obeys the square root law. The derived time dependence of the correlation radius makes it possible to estimate the degree of enlargement of the domain structure and determine the fundamental parameter — the radius of interatomic interaction. Due to the formation of domains immediately after rapid quenching this method allows the use of electric fields of small amplitude. A similar effect allows us to direct the process of ordering the system to the formation of domains of the desired type. It is expected that this approach will reduce the risk of crystal destruction and significantly increase the precision of the RDS obtained.
Speaker: Olga Mazur (Institute for Physics of Mining Proceses of the NAS of Ukraine) -
10:40
Circular stripe domains in a vertically stacked magnetic heterostructures 20m
Magnetic vortex is known to form a ground state of magnetic nanodisk with easy-plane anisotropy [1]. A perpendicularly magnetized disk in a nanostack can also support the vortex state due to the interlayer exchange coupling with the vortex state thick layer [2].

Fig.1: Phase diagram of different states on Co disk. The following parameters of the Co disk were used in OOMMF simulations: disk radius $R = 500$ nm, exchange constant $A = 2\times10^{-11}$ J/m, saturation magnetization $Ms = 5\times10^5$ A/m, easy-normal anisotropy $K = 2\times10^5$ J/m$^3$.Here we predict formation of circular stripe domains in the cylinder nanopillar of vertically stacked magnetic heterostructure. Using OOMMF micromagnetic simulations [3] we model the three-layer heterostructure where the topological magnetization texture is imprinted into an out-of-plane magnetized material through stacking three layers with in-plane magnetization (Py master layer), nonmagnetic material (Pd spacer layer) and out-of-plane magnetization (Co slave layer, the sample). The phase diagram of equilibrium magnetisation states in the sample disk is computed in a wide range of the coupling parameter for different thicknesses of the sample layer (see Fig.1): (i) The cone phase is realized for a weak coupling; within this phase the cone-state light vortex has a structure, similar to ones in easy-plane magnets under the action of perpendicular magnetic field [4]. (ii) The opposite limit case of strong coupling results to the vortex phase, which structure mimics the master layer vortex texture. (iii) The appearance of the new phase with the circular stripe domains is a key finding of the current study. This circular stripe phase is realized for the intermediate coupling parameters. The modulation instability of the cone state is triggered by the nonlocal magnetostatic interaction, which results in the generation of the stable equilibrium magnetization texture in the form of circular stripes domains. The number of stripes is controlled by both coupling parameters and the sample thickness. The phase transition between different states is described analytically using a simple Ansatz model and corresponds to the full scale micromagnetic simulations. The variety of magnetization textures with well-defined phases corresponds to the experimentally observed vortex and donut states in [2].
The possibility to switch between different topologically nontrivial states allows for engineering magnetic textures with possible applications in spintronic devices.References
[1] A. Hubert and R. Schäfer, Magnetic domains: the analysis of magnetic microstructures, Springer (2009)
[2] R. Streubel et al, Scientific Reports 5, 8227 (2015)
[3] Object Oriented MicroMagnetic computing Framework (OOMMF)
[4] B. A. Ivanov and D. D. Sheka, Low Temperature Physics 21, 881 (1995)Speaker: Oleksandr Zaiets (Taras Shevchenko National University of Kyiv) -
11:00
Coffee break 20m
-
11:20
Magnetic field-induced phase transitions in antiferromagnetic rings 20m
An emerging field of curvilinear magnetizm brings about new geometry-induced phenomena in usual magnetic materials, balancing between fundamental research, material sciences and technologies [1]. Modern technological advances allow to consider antiferromagnets (AFMs) as promising building blocks for spintronic and spin-orbitronic applications [2]. In this respect, curvilinear spin chains with AFM coupling are of fundamental interest as simplest systems possessing interplay between geometry and magnetic subsystem.
Here, we analyze the ground states of AFM ring with the nearest-neighbour Heisenberg exchange and strong single-ion anisotropy in the presence of external magnetic field, which is normal to the ring plane. We consider collinear two-sublattice 1D curved AFM spin chain with even number of spins. The hard axis of anisotropy is oriented tangentially to the chain. Within the classical continuum approach [3], its magnetic state is determined by the vector fields of Néel and ferromagnetism. In the ground state, the Néel vector is oriented perpendicularly to the ring plane (binormal state, see Fig.1) [3,4]. The magnetic field applied along the ring normal allows to observe spin-flop and spin-flip orientational phase transitions. We determine the dependency of spin-flop and spin-flip transition fields on the ring curvature. There is a critical curvature ($\kappa_c$), separating two topologically different ground states above spin-flop. The first one with the Néel order parameter within the normal plane is mainly determined by the anisotropy at small curvatures (normal state, see Fig.1). The second ground state at large curvatures is represented by oninon ordering of the Néel vector (onion state, see Fig.1). With the applied fields $h>h^0$, Néel order parameter vanishes (ferromagnetic state). The phase diagram of AFM as a function of applied field intensity is presented in Fig.1: all analytical predictions are well-confirmed by the SLaSi spin-lattice simulations [5].
Fig.1: phase-diagram.jpg should be here, with
caption: "Phase diagram of equilibrium magnetization states of antiferromagnetic ring; $h^{sf}_0$ is the spin-flop transition field in the bulk, $\kappa$ is the ring curvature, $\ell = 5 a_0$ is the magnetic length, with $a_0$ being the lattice constant. Symbols correspond to spin-lattice simulation data, solid lines describe analytically calculated boundary between states"[1] E.Vedmedenko et al, Journal of Physics D: Applied Physics 53, 453001(2020).
[2] V. Baltz et al, Reviews of Modern Physics 90, 015005 (2018)
[3] O. V. Pylypovskyi et al, Nano Letters 20, 8157 (2020)
[4] S. Castillo-Sepulveda et al, Physical Review B 96, 024426 (2017)
[5] [SLaSi spin–lattice simulations package]Speaker: Yelyzaveta A. Borysenko (Taras Shevchenko National University of Kyiv, 01601 Kyiv, Ukraine) -
11:40
Size Characteristics for the Hyperbranched Polymers 20m
In the present work we calculated size characteristics of periodic hyperbranched polymers in dilute solution in the vicinity of the $\theta$ point using the continuous chain model. This model in its Gaussian approximation allows to receive exact solutions. Both the gyration radius and the hydrodynamic radius were calculated for the bottle-brush polymer and a tree-like one. We considered the size ratios $\rho=\frac{\sqrt{\langle R_g^2\rangle}}{\langle R_h\rangle}$ and $g = \frac{\langle R_{g}^2\rangle}{\langle R_{g,chain}^2\rangle}$, that allows to describe the characteristic sizes of this topologies. This types of ratios allow to shed some light on visco-elastic properties of polymer solutions.
Speaker: Khristine Haydukivska (Institute for Condensed Matter Physics NAS Ukraine)
-
09:00
-
12:00
→
12:45
Physics of Biological Macromolecules
-
12:00
Conformational solitons in DNA macromolecule 45m
Accuracy of genetic information implementation in living cells is largely due to the peculiarities of the structure and variability of DNA double helix. The regulation of genetic activity, stability and security of genetic texts, reading and translation of genetic information, all of these important biological processes take place because of the unique properties of the DNA double helix, which distinguish them from other cellular molecules. One of the key properties of DNA molecule is the polymorphism of its double helix, through which this molecule has the ability to change the structure on some definite sites under the influence of external factors or depending on the nucleotide sequence. Arising in this case localized deformations can have a sufficiently large amplitude of structural element deviations from their equilibrium positions in the double helix and are the conformational solitons by their nature. Such localized deformations cannot be understood within the framework of the elastic rod model, which is suitable for studying DNA mechanics in a harmonic approximation. On the other hand, the all-atomic modelling cannot frequently explain the mechanism of DNA double helix deformations due to the complex character of macromolecule structure changes and many degrees of freedom of the double helix.
The report presents an approach for the consideration of conformation-dependent deformations in DNA macromolecule. The transformation of the DNA structure is considered in the frame of the two-component model. One model component (external) describes the macromolecule deformation as in the model of the elastic rod, another component (internal) - the conformation changes of the macromolecule monomer units. Both components are considered as interconnected on the paths of certain conformational transformation. The approach provides the possibility to predict the sizes and energies of local deformations of the double helix and explained the appearance of solitary excitations in the DNA chain at the location of some definite nucleotide sequences.
The results obtained make it possible to uniformly interpret the long-range soliton effects in the DNA chain, the deformability of specific DNA sequences, as well as the threshold nature of the effects of DNA unzipping and overstretching. The presented results can also be useful for a deeper understanding of the mechanisms of DNA functioning in the cell, and for the development of modern technologies in the fields of molecular medicine, DNA engineering, smart materials and nanodevices.The lecture is dedicated to the memory of A.S. Davydov - an outstanding scientist, academician of the National Academy of Sciences of Ukraine, Hero of Socialist Labor, and director of the Institute of Theoretical Physics of the National Academy of Sciences of Ukraine (1973-1988).
Speaker: Prof. Sergej Volkov (Bogolyubov Institute for Theoretical Physic)
-
12:00
-
12:45
→
14:00
Lunch 1h 15m
-
14:00
→
16:50
Physics of Biological Macromolecules
-
14:00
Multiscale simulation methods and their applications in nucleic acid studies 45m
After almost seventy years from the discovery of DNA double helix structure, we know very much about nucleic acid organization and functions. However, there are still many structural and dynamical features - at different spatial and time scales - that have to be understood better. Molecular simulations are essential to understand many properties at the molecular level. With a fast increase in the computer power together with method and software development, systems over increasing sizes and longer and longer timescales can be simulated. However, studies of DNA at the atomistic level have a practical maximum size allowing a few nucleosome core particles, on the microsecond time scale to be studied. To reach larger spatial and longer temporal time scales, necessary when studying many of the biological problems involving DNA (e.g. those connected to DNA flexibility, or to chromatin folding etc.) all-atom simulations are far too expensive. It is necessary to coarsen the description of the system of interest, by removing many details non-relevant to the phenomenon under investigation [1-4]. In this talk I will present selected coarse-grain (CG) models, some of which can be applied to the double helix conformation as well as to other nucleic acid structural motifs found in the cells, like DNA quadruplexes [5-6]. Special attention will be given to the methods that can be used to study the counter-ions interactions with this highly charged poly-ion.
References:
[1] Mocci F, Laaksonen A (2012). Insight into nucleic acid counterion interactions from inside molecular dynamics simulations is “worth its salt”. Soft Matter, 8, 9268-9284
[2] Potoyan DA, Savelyev A, Papoian G A (2013) Recent successes in coarse-grained modeling of DNA. WIREs Computational Molecular Science, 3, 69-8
[3] Dans PD, Walther J, Gómez H, Orozco M (2016) Multiscale simulation of DNA, Current Opinion in Structural Biology, 37, 29-45
[4] Sun T, Mirzoev A, Minhas V, Korolev N, Lyubartsev AP, Nordenskiöld L (2019) , A multiscale analysis of DNA phase separation: from atomistic to mesoscale level, Nucleic Acids Research, 47:11, 5550–5562,
[5] Rebič M, Mocci F, Lyubartsev AP, Uličný J, Laaksonen A (2017) Coarse-Grained Simulation of Rodlike Higher-Order Quadruplex Structures at Different Salt Concentrations ACS Omega 2 (2), 386-396
[6] Rebič M, Mocci F, Laaksonen A, Uličný J (2015) Multiscale simulations of human telomeric G-quadruplex DNA. The Journal of Physical Chemistry B 119 (1), 105-113Speaker: Dr Francesca Mocci (Chemistry and Geological Science Department, University of Cagliari) -
14:45
Excess Thermodynamic Properties of Binary Liquid Mixtures of Butanol Isomers with Di-n-Butyl Ether at 298.15 K, 0.1 MPa 20m
Binary liquid mixtures of alcohols and ethers are of importance as potential biofuels or additives for internal combustion engines,[1] and have also attracted fundamental interest as model liquid systems containing one component (the alcohol) that can strongly self-associate through hydrogen bonding (HB), and one that cannot self-associate via HBs (ether), yet can interact strongly with the former as HB acceptor.[2] The excess thermodynamic properties of these mixtures, specifically the excess molar enthalpies and volumes (HE and VE), have been extensively measured.[1-3] Butanol isomer + di-n-butyl ether (DBE) binary mixtures, in particular, show interesting volumetric differences, with VE changing from negative (1- and iso-butanol) to positive (2- and tert-butanol) with increasing butanol alkyl group branching. Representative 1- and 2-butanol + DBE mixtures were studied, for the first time, by atomic-resolution classical Molecular Dynamics (MD) computer simulations. The simulations reveal decided differences in the degree of self-association of the two butanol isomers and support existing interpretations of the HE and VE in a general sense, but also suggest that more subtle differences in H-bonded topologies may contribute significantly to the anomalous volumetric properties of these mixtures.[4]
Fig. 1. MD computer simulation configurations of equimolar mixtures of 1- or 2-butanol with DBE. Ether molecules are omitted and hydroxyl (-OH) groups shown using a space-filling (red and white spheres) representation in order to highlight the differences in HB topologies. Simulation cell edges are shown in blue.References:
[1] (a) Rezanova, E. N.; Kammerer, K.; Lichtenthaler, R. N. J. Chem. Eng. Data 1999, 44, 1235-1239. (b) Alaoui, F. E. M.; Montero, E. A.; Brazile, J. -P.; Aguilar, F.; Boned, C. J. Chem. Thermodynamics, 2011, 43, 1768-1774.
[2] (a) Motoyama, I.; Jarboe, C. H. J. Phys. Chem. 1967, 71 (8), 2723-2726. (b) Pathak, G.; Pradhan, S. Proc. Indian Acad. Sci. (Chem. Sci.) 1988, 100 (6), 519-523. (c) Lechter, T. M.; Govender, P. U. Fluid Phase Equilibria, 1997, 140, 207-220.
[3] (a) Patil,K. R.; Pathak, G.; Pradhan, S. D. Proc. Indian Acad. Sci. (Chem. Sci.) 1989, 101 (5), 443-447. (b) Kammerer, K.; Licthenthaler, R. N. Thermochim. Acta 1998, 310 (1-2), 61-67. (c) Bernazzani, L.; Carosi, M. R.; Duce, C.; Gianni, P.; Mollica, V. J. Solution Chem. 2006, 35 (11), 1567-1585.
[4] Engelbrecht, L.; Farris, R.; Vasiliu, T.; Demurtas, M.; Laaksonen, A.; Piras, A.; Cesare Marincola, F.; Porcedda, S.; Mocci. F. Submitted for publication.Speaker: Leon Engelbrecht (University of Cagliari, Italy) -
15:05
Partitioning electrostatic molecular properties into the localized contributions 20m
Approximations for the molecular dipole moment vector as well as for the spatial distributions of the charge density and electrostatic potential in terms of localized contributions associated with individual atoms and covalent bonds are discussed. The application of recently proposed CLPO method [1] yielding the chemically meaningful set of localized orbitals particularly suitable for this application is considered. The role of the atomic lone electron pairs and bonding orbitals charge densities is highlighted in achieving an accurate decomposition of electrostatic molecular properties into the localized contributions. Comparison with simple point-charge methods, traditionally used in force fields for molecular dynamics simulations, is made. Impact of accuracy of the considered decompositions on electrostatic component of intermolecular interaction energy is quantified for the standard test set of non-covalently bounded complexes GMTKN55 [3].
Acknowledgements. The work has been partially supported by the National Research Foundation of Ukraine (project No. 101/01.2020).[1] T. Y. Nikolaienko and L. A. Bulavin, Int. J. Quantum Chem. (2019), 119: e25798.
[2] L.Goerigk, A.Hansen, C.Bauer, S.Ehrlich, A.Najibi and S.Grimme, Phys.Chem.Chem.Phys. (2017), 19:32184.Speaker: Tymofii Nikolaienko (Taras Shevchenko National University of Kyiv) -
15:25
Coffee break 25m
-
15:50
Dynamics of K$^+$ counterions around DNA double helix in the external electric field: a molecular dynamics study 20m
The structure of DNA double helix is stabilized by metal counterions condensed to a diffuse layer around the macromolecule. The dynamics of counterions in real conditions is governed by the electric fields from DNA and other biological macromolecules. In the present work, the molecular dynamics study was performed for the system of DNA double helix with neutralizing K$^+$ counterions and for the system of KCl salt solution in an external electric field of different strength (up to 32 mV/ Å). The analysis of ionic conductivities of these systems has shown that the counterions around the DNA double helix are slowed down compared with the KCl salt solution. The calculated values of ion mobility are within (0.05–0.4) mS/cm depending on the orientation of the external electric field relative to the double helix. Under the electric field parallel to the macromolecule, K$^+$ counterions move along the grooves of the double helix staying longer in the places with narrower minor groove. Under the electric field perpendicular to the macromolecule, the dynamics of counterions is less affected by DNA atoms, and starting with the electric field values about 30 mV/ Å the double helix undergoes a phase transition from a double-stranded to a single-strand state.
Speaker: Dr Oleksii Zdorevskyi (Bogolyubov Institute for Theoretical Physics ) -
16:10
Low-frequency modes of water vibrations in the minor groove of DNA double helix 20m
Water and ions around DNA macromolecule are paramount for the stability of the double helix structure and found to mediate the vital biological process such as nucleic-protein recognition, and the interaction with the biologically active compounds. DNA interacts strongly with surrounding water molecules and counterions making the hydration shell with different structural and dynamical features in different regions of the double helix (minor and major grooves, phosphate groups). In the DNA minor groove water molecules are highly ordered and in the case of AATT nucleotide sequence, the spine of hydration is formed [1]. In the present research [2], the vibrations of hydration spine have been studied to establish the mode of translational vibrations of water molecules in the DNA low-frequency spectra ($<$ 200 cm$^{-1}$). Within the framework of the developed phenomenological model, based on the approach of DNA conformational vibrations [3], the modes of water vibrations and DNA structural elements have been determined. The calculations for the case of DNA fragment CGCGAATTCGCG have shown that the frequencies of water vibrations are about 185 $\pm$ 20 cm$^{-1}$ depending on nucleotide sequence. The obtained mode of water vibrations higher than the modes of internal conformational vibrations of DNA and observed in the same region of the vibrational spectra as translation vibrations of water molecules in the bulk phase. To distinguish the vibrations of water molecules from those in the bulk, the dynamics of DNA with heavy water (D$_2$O) has been considered. The estimations have shown that in the case of D$_2$O the frequency of vibrations decreases for about 10 cm$^{-1}$ that may be used to identify the vibrations of water spine of the DNA minor groove experimentally.
- Horace R Drew and Richard E Dickerson. Structure of a B-DNA dodecamer: III. Geometry of hydration. Journal of molecular biology, 151(3):535–556, 1981.
- T.L. Bubon and S.M. Perepelytsya. Low-frequency vibrations of water molecules in minor groove of the DNA double helix. arXiv preprint arXiv:2010.15967, 2020. (submitted to European Physical Journal E)
- S.N. Volkov and A.M. Kosevich. Conformation oscillations of DNA. Molekuliarnaia biologiia, 21(3):797–806, 1987.
Speaker: Ms Tatyana Bubon ( Bogolyubov Institute for Theoretical Physics ) -
16:30
Potential electron scattering by the threonine andtyrosine amino acid biomolecules 20m
Our report is devoted to a brief exposition of methodics of the description of potential electron scattering on complex molecules. In the Additivity Rule approach the differential and integral cross-sections of elastic electron scattering by amino acids biomolecules, threonine and tyrosine are calculated.
Expressions for amplitudes and cross sections of electron scattering on molecules in the independent atoms model were given. The Additivity Rule approach was described. Expressions for amplitudes and differential cross sections of electron scattering on the atoms of which the molecule consists were given. The scattering phase shifts are calculated in the optical potential method of the ELSEPA program.
Theoretical calculations of differential cross sections of electron scattering on biomolecules (Threonine and Tyrosine) were made with energy levels of 20, 40, 60, 75, 100, 150 eV. Theoretical calculations of integral cross sections of electron scattering on same biomolecules were made as well. From the obtained results, we saw that behaviour of differential cross sections of electron scattering is pretty smooth and is characterized with wide graph minimum. This minimum gets wider with the increase of collision energy.Speaker: Mr Oleksandr Vasyliev (Institute of Electron Physics)
-
14:00
-
16:50
→
17:00
Closing of the conference
-
09:00
→
12:00